��Ŀ����
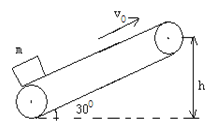
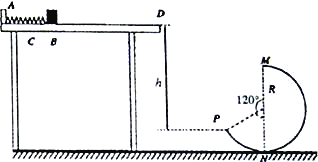
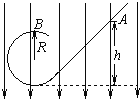
����Ŀ����ͼ������Ϊm��С���б�����h���ɾ�ֹ���£�Ȼ������ֱԲ������ڲ��˶�����֪Բ����İ뾶ΪR������һ��Ħ���������������ٶ�Ϊg��������˵����ȷ���ǣ� ��

A����h=2Rʱ��С��ǡ���ܵ�����ߵ�M
B����h=2Rʱ��С����Բ�ĵȸߴ�Pʱ�Թ��ѹ��Ϊ2mg
C����h��Rʱ��С�����˶������в���������
D����h=Rʱ��С������͵�Nʱ�Թ��ѹ��Ϊ2mg
���𰸡�BC
��������
���������ʹС���ܹ�ͨ��Բ�����ߵ�M����ôС������ߵ�ʱӦ����ǡ�����������������Ϊ����������������������Ĺ�ʽ������ô�ʱ����С���ٶȣ����ɻ�е���غ������ø߶�h������������Ҳ����Բ�����Բ���·�����������˶���
�⣺A����Բ�������ߵ�M����ţ�ٵڶ������У�mg=m![]() ��
��
�ã�v0=![]()
���ݻ�е���غ�ã�mgh=mg2R+![]()
��ã�h=2.5R����A����
B����h=2Rʱ��С����Բ�ĵȸߴ�Pʱ�ٶ�Ϊv�����ݻ�е���غ�ã�mg2R=mgR+![]()
С����Pʱ���У�N=m![]()
������� N=2mg����֪С����Բ�ĵȸߴ�Pʱ�Թ��ѹ��Ϊ2mg����B��ȷ��
C����h��Rʱ�����ݻ�е���غ��֪С����Բ�����Բ���·�����������˶������˶������в�������������C��ȷ��
D����h=Rʱ����С������͵�Nʱ�ٶ�Ϊv�䣬���У�
mgR=![]()
��Բ�����͵㣬�У�N�䩁mg=m![]()
��ã�N��=3mg����С������͵�Nʱ�Թ��ѹ��Ϊ3mg����D����
��ѡ��BC��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�