题目内容
3.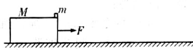 如图所示,水平地面上一质量M=10.0kg、高h=1.25m的木箱处于静止状态,在其上面最右端放一质量m=1.0kg可以视为质点的物块.已知物块与木箱、木箱与地面的滑动摩擦因数分别为μ1,μ2,且μ1=μ2=0.1,现在给木箱一个F=32N水平向右的力,使木箱和物块同时从静止开始运动,t=2s时物块脱离木箱.(取g=10m/s2)求:
如图所示,水平地面上一质量M=10.0kg、高h=1.25m的木箱处于静止状态,在其上面最右端放一质量m=1.0kg可以视为质点的物块.已知物块与木箱、木箱与地面的滑动摩擦因数分别为μ1,μ2,且μ1=μ2=0.1,现在给木箱一个F=32N水平向右的力,使木箱和物块同时从静止开始运动,t=2s时物块脱离木箱.(取g=10m/s2)求:(1)物块刚落地时的动能;
(2)物块脱离木箱时木箱的速度;
(3)物块刚落到地面时,物块到箱底左端的距离.
分析 (1)对物块受力分析,由牛顿第二定律可求得物体的加速度,再由运动学公式可求得速度,对平抛过程由动能定理可求得落地时的速度;
(2)对木箱受力分析,由牛顿第二定律及运动学公式可求得木箱的速度;
(3)物块脱离木箱后做平抛运动,由平抛运动可知物体下落时间,再对木块分析,由牛顿第二定律及运动学公式可求得木箱的位移,即可求得位移差值.
解答 解:(1)设物块在木箱上运动时的加速度为a1,刚脱离木箱时的速度为v1,则有:
μ1mg=ma;
v1=a1t
从脱离木箱到落地由动能定理可得:
mgh=$\frac{1}{2}$mv12
联立解得:EK=14.5J;
(2)设物块在木箱上运动时,木箱的加速度为a2,物块脱离木箱时木箱的速度为v2,则有:
F-μ2(M+m)g-μ1mg=Ma2
v2=a2t
联立解得:v2=4m/s;
(3)物块脱离木箱后做平抛运动,则有:
h=$\frac{1}{2}$gt′2
x1′=v1t′
设物块脱离木箱后木箱的加速度为a2′,则有:
F-μ2Mg=Ma2′
x2′=v2t′+$\frac{1}{2}$a2′t′2
△x=x2′-x1′
联立解得:△x=1.275m;
答:(1))物块刚落地时的动能14.5J;
(2)物块脱离木箱时木箱的速度为4m/s;
(3)物块刚落到地面时,物块到箱底左端的距离1.275J.
点评 本题考查动能定理、牛顿第二定律及平抛运动规律,要注意明确加速度的桥梁作用,明确物体的运动过程,做好受力分析.

练习册系列答案
相关题目
13.下列说法不正确的是( )
| A. | 电场强度E=$\frac{F}{q}$和B=$\frac{F}{IL}$磁感应强度定义物理量的方法是比值定义法 | |
| B. | 互感现象是变压器工作的基础 | |
| C. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这应用了“微元法” | |
| D. | 法拉第最先引入“场”的概念,并最早发现了电流的磁效应现象 |
14.一列在y轴上振动的简谐横波沿x轴正方向传播,t=0时,平衡位置在x=0处的质元a位于平衡位置且向上振动,平衡位置在x=10.5m处的质元b位于波谷;t=1.0s时,质元a恰好第一次位于波峰,则( )
| A. | 该波的波长可能为14m | |
| B. | 该波的波速可能为10.5m/s | |
| C. | 该波由a传播到b可能历时7s | |
| D. | t=1.5s时,质元a的速度方向和加速度方向相同 |
18.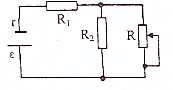 在如图所示的电路中,若滑动变阻器的滑动端向下移动时,则( )
在如图所示的电路中,若滑动变阻器的滑动端向下移动时,则( )
 在如图所示的电路中,若滑动变阻器的滑动端向下移动时,则( )
在如图所示的电路中,若滑动变阻器的滑动端向下移动时,则( )| A. | R两端的电压增大 | B. | R两端的电压减小 | ||
| C. | 通过R的电流强度不变 | D. | 通过R的电流强度增大 |
8.如图甲所示,矩形线圈ABCD通过滑环与理想变压器相连,触头P可移动,副线圈所接电阻R=10Ω,表均为理想交流电表.E、F两端输出电压如图乙所示,下列说法正确的是( )
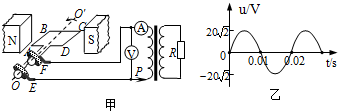

| A. | 此u-t图是从中性面开始计时的 | |
| B. | P上移时,电流表示数减小 | |
| C. | t=0时,电压表示数为0V | |
| D. | 当原、副线圈匝数比为2:1时,电阻上消耗的功率为10W |
15.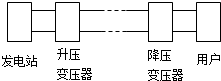 如图为远距离输电示意图,升压变压器与降压变压器的匝数比分别为1:100和100:1,发电站输出电压为u=250$\sqrt{2}$sin100πt(V),下列说法正确的是( )
如图为远距离输电示意图,升压变压器与降压变压器的匝数比分别为1:100和100:1,发电站输出电压为u=250$\sqrt{2}$sin100πt(V),下列说法正确的是( )
 如图为远距离输电示意图,升压变压器与降压变压器的匝数比分别为1:100和100:1,发电站输出电压为u=250$\sqrt{2}$sin100πt(V),下列说法正确的是( )
如图为远距离输电示意图,升压变压器与降压变压器的匝数比分别为1:100和100:1,发电站输出电压为u=250$\sqrt{2}$sin100πt(V),下列说法正确的是( )| A. | 用户得到的交变电压频率为50Hz | |
| B. | 用户得到的交变电压有效值为250V | |
| C. | 用户得到的交流电压有效值小于250V | |
| D. | 输送过程中电能的损耗主要来自变压器原、副线圈的发热 |
13.在牛顿第二定律公式F=kma中,比例系数k的数值( )
| A. | 在任何情况下都等于1 | |
| B. | 是由质量m、加速度a和力F三者的大小所决定的 | |
| C. | 是由质量m、加速度a和力F三者的单位所决定的 | |
| D. | 在国际单位制中一定不等于1 |
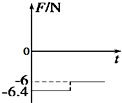
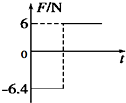
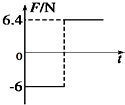
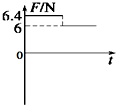
 如图所示,倾角为37°的长斜面固定在水平地面上,质量为1kg的滑块以初速度v0从斜面底端沿斜面向上滑行,取初速度方向为正方向,已知滑块与斜面间的动摩擦因数为0.8,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.则该滑块所受摩擦力Ff随时间变化的图象是( )
如图所示,倾角为37°的长斜面固定在水平地面上,质量为1kg的滑块以初速度v0从斜面底端沿斜面向上滑行,取初速度方向为正方向,已知滑块与斜面间的动摩擦因数为0.8,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.则该滑块所受摩擦力Ff随时间变化的图象是( )