题目内容
【题目】如图所示为一列简谐横波沿x轴传播在t=0(实线)和t=0.5s(虚线)时刻的波形图。
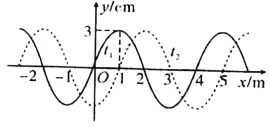
(1)若t=0时刻,x=2.5m处质点正沿y轴负方向振动,求该质点第一次回到t=0时刻的位置所经过的最长时间;
(2)若波动的周期T≤0.5s≤2T,则在1s内波形传播的距离为多少?
【答案】(1)![]() (2)10m或14m
(2)10m或14m
【解析】
①据在t=0时刻,x=2.5m处的质点向y轴负方向运动,根据波形平移法得到该波的传播方向;由两个时刻的波形可知时间与周期的关系,求出周期的通项,根据周期通项,读出波长,求出波速。
②简谐波传播过程中,振动在一个周期内传播一个波长的距离。根据波形的平移法可知,若波向左传播,且T<△t<2T,则波传播的距离是 1![]() λ;若波向右传播,且T<△t<2T,波传播的距离是1
λ;若波向右传播,且T<△t<2T,波传播的距离是1![]() λ,从而求得波速,进而即可求解1s内波形平移的距离。
λ,从而求得波速,进而即可求解1s内波形平移的距离。
(1)已知在t=0时刻,x=2.5m处的质点向y轴负方向运动,波形向左平移,所以该波沿x轴的负方向传播。结合图像可知,该质点回到t=0时刻的位置波形传播的最小距离为x=1m,波传播的速度![]() (k=0,1,2,…),k=0时波速最小,最小速度为v=6m/s;x=2.5m处质点回到t=0时刻的位置所用最长时间
(k=0,1,2,…),k=0时波速最小,最小速度为v=6m/s;x=2.5m处质点回到t=0时刻的位置所用最长时间![]()
(2)由于T≤0.5s≤2T,若波沿x轴正向传播,则0.5s内波传播的距离为x1=5m;波在1s内传播的距离为10m;若波沿x轴负向传播,则0.5s内波传播的距离为x2=7m;波在1s内传播的距离为14m;

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目