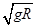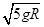题目内容
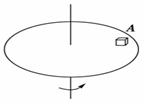
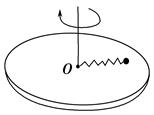
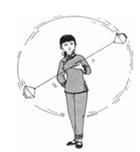
在光滑平面中，有一转动轴垂直于此平面，交点O的上方h处固定一细绳的一端，绳的另一端固定一质量为m的小球B，绳长AB＝l>h，小球可随转动轴转动并在光滑水平面上做匀速圆周运动，如图所示，要使小球不离开水平面，转动轴的转速的最大值是( )．
A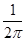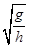．  | B．π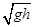 | C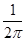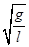． | D．2π  |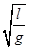
A
如图所示，
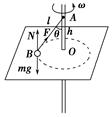
以小球为研究对象，小球受三个力的作用，重力mg、水平面支持力N、绳子拉力F.在竖直方向合力为零，在水平方向所需向心力为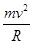
，而R＝htan θ，得Fcos θ＋N＝mg
Fsin θ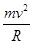＝＝mω2R＝m4π2n2R＝m4π2n2htan θ
当球即将离开水平面时，N＝0，转速n有最大值．
即mg－m4π2n2h＝0，n＝ .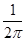
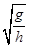以小球为研究对象，小球受三个力的作用，重力mg、水平面支持力N、绳子拉力F.在竖直方向合力为零，在水平方向所需向心力为
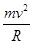，而R＝htan θ，得Fcos θ＋N＝mgFsin θ＝
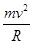＝mω2R＝m4π2n2R＝m4π2n2htan θ当球即将离开水平面时，N＝0，转速n有最大值．
即mg－m4π2n2h＝0，n＝
.
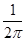
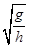练习册系列答案
阅读快车系列答案
相关题目
