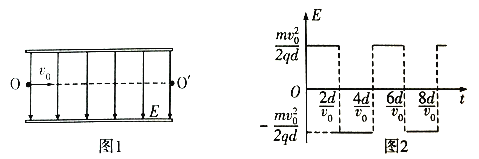
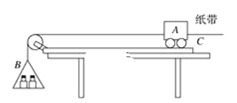
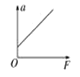题目内容
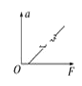
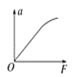
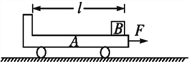
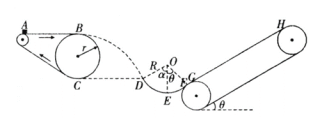
【题目】科技馆有一套儿童喜爱的机械装置,其结构简图如下:传动带AB部分水平,其长度L=1.2m,传送带以3m/s的速度顺时针匀速转动,大皮带轮半径r=0.4m,其下端C点与圆弧轨道DEF的D点在同一水平线上,E点为圆弧轨道的最低点,圆弧EF对应的圆心角θ=![]() 且圆弧的半径R=0.5m,F点和倾斜传送带GH的下端G点平滑连接,倾斜传送带GH长为x=4.45m,其倾角θ=
且圆弧的半径R=0.5m,F点和倾斜传送带GH的下端G点平滑连接,倾斜传送带GH长为x=4.45m,其倾角θ=![]() 。某同学将一质量为0.5kg且可以视为质点的物块静止放在水平传送带左端A处,物块经过B点后恰能无碰撞地从D点进入圆弧轨道部分,当经过F点时,圆弧对物块支持力N=29.0N,然后物块滑上倾斜传送带GH。已知物块与所有的接触面间的动摩擦因数均为μ=0.5,重力加速度g=10m/s2,sin
。某同学将一质量为0.5kg且可以视为质点的物块静止放在水平传送带左端A处,物块经过B点后恰能无碰撞地从D点进入圆弧轨道部分,当经过F点时,圆弧对物块支持力N=29.0N,然后物块滑上倾斜传送带GH。已知物块与所有的接触面间的动摩擦因数均为μ=0.5,重力加速度g=10m/s2,sin![]() =0.6,cos
=0.6,cos![]() =0.8,
=0.8,![]() ,求:
,求:
(1)物块由A到B所经历的时间;
(2)DE弧对应的圆心角![]() 为多少;
为多少;
(3)若要物块能被送到H端,则倾斜传动带顺时针运转的速度最小值vmin为多少。
【答案】(1)0.7s(2)![]() (3)4m/s
(3)4m/s
【解析】
(1) 放在水平传送带上的物体受到重力、支持力和摩擦力的作用,摩擦力提供水平方向的加速度,由牛顿第二定律得:
![]()
所以
![]()
物体加速到3m/s的时间:
![]()
在加速阶段的位移
![]()
物体做匀速直线运动的时间
![]()
物块由A到B所经历的时间
![]()
(2)若物体能在B点恰好离开传送带做平抛运动,则满足:
![]()
所以
![]()
所以物体能够在B点离开传送带做平抛运动,平抛运动的时间:
![]()
到达D点时物体沿竖直方向的分速度
![]()
到达D点时物体的速度与水平方向之间的夹角
![]()
所以
![]()
即DE弧对应的圆心角α为![]()
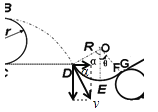
(3)物体在F点时,支持力与重力的分力提供向心力得
![]()
代入数据得
![]()
物体在倾斜的传送带上受到重力、支持力和滑动摩擦力的作用,滑动摩擦力:
![]()
重力沿斜面向下的分力
![]()
可知物体不可能相对于传送带静止,所以物体在传送带上将一直做减速运动.物体恰好到达H点时的速度为0,若传送带的速度小于物体在F点的速度,则物体先相对于传送带向上运动,受到的摩擦力的方向向下;当物体的速度小于传送带的速度后,受到的摩擦力的方向向上,物体继续向上做减速运动,加速度的大小发生变化,设物体恰好能到达H点时,传送带的速度是vmin,且vmin<v3,物体到达H点的速度为0,物体的速度大于传送带的速度时,物体受到的摩擦力的方向向下,此时:
![]()
则
![]()
物体的速度小于传送带的速度时,物体受到的摩擦力的方向向上,则:
![]()
物体向上的减速运动若反过来看,也可以是向下是加速运动,初速度为0,末速度为v3,设下面的一段时间为t4,上面的一段时间为t5,可得:
![]()
![]()
![]()
联立以上三式,代入数据得
![]()