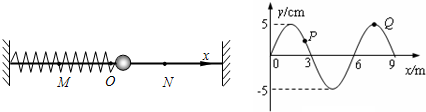题目内容
 一水平弹簧振子做简谐运动,其位移和时间关系如图所示.
一水平弹簧振子做简谐运动,其位移和时间关系如图所示.(1)求t=0.25×10-2 s时的位移.
(2)从t=0到t=8.5×10-2 s的时间内,质点的路程、位移各为多大?
分析:(1)由图读出周期T,由公式ω=
求出圆频率?,即可写出振动方程,再求出t=0.25×10-2 s时的位移.
(2)根据t=8.5×10-2 s与周期的关系,结合一个周期内质点通过的路程是4个振幅,求路程,并确定位移.
| 2π |
| T |
(2)根据t=8.5×10-2 s与周期的关系,结合一个周期内质点通过的路程是4个振幅,求路程,并确定位移.
解答:解:(1)由图知,T=2×10-2s,A=2cm,则ω=
=100πrad/s
所以振子的振动方程为x=-Acosωt=-2cos100πt(cm)
当t=0.25×10-2 s时位移为x=-2cos100π×0.25×10-2=-1.41cm
(2)t=8.5×10-2 s时,x=-2cos100π×8.5×10-2=0
∵n=
=
=4.25T
所以在这段时间内能过后路程为S=4.25×4A=34cm
答:
(1)t=0.25×10-2 s时的位移为-1.41cm.
(2)从t=0到t=8.5×10-2 s的时间内,质点的路程、位移各为34cm,0.
| 2π |
| T |
所以振子的振动方程为x=-Acosωt=-2cos100πt(cm)
当t=0.25×10-2 s时位移为x=-2cos100π×0.25×10-2=-1.41cm
(2)t=8.5×10-2 s时,x=-2cos100π×8.5×10-2=0
∵n=
| t |
| T |
| 8.5×10-2 |
| 2×10-2 |
所以在这段时间内能过后路程为S=4.25×4A=34cm
答:
(1)t=0.25×10-2 s时的位移为-1.41cm.
(2)从t=0到t=8.5×10-2 s的时间内,质点的路程、位移各为34cm,0.
点评:本题考查运用数学知识处理物理问题的能力,关键要能写出振动方程.书写振动方程抓住三要素:振幅、圆频率和初相位.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 A.选修3-3
A.选修3-3