题目内容
如图所示,一弹簧振子在光滑水平面内做简谐振动,O为平衡位置,A,B为最大位移处,测得振子由A点从静止开始振动到第二次经过平衡位置所用时间为t秒,在O点正上方C处有一个小球,现使振子由A点,小球由C点同时从静止释放,它们恰好到O点处相碰,试求小球所在C点距水平面的高度H是多少?(该地的重力加速度为g)


分析:根据题意,弹簧振子由A点从静止开始振动到第二次经过平衡位置所用时间为t秒,则有
T=t,求出弹簧振子的周期T.小球由C点同时从静止释放做自由落体运动,振子由A点同时释放,它们恰好到O点处相碰时,两者运动的时间相同.根据弹簧振子振动的周期性,确定出振子运动的时间,由运动学位移公式求出H.
| 3 |
| 4 |
解答:解:据题意,弹簧振子由A点从静止开始振动到第二次经过平衡位置所用时间为t秒,则有
T=t
得到T=
t
当振子与小球恰好到O点处相碰时,振子运动的时间为t0=
(2K+1),K=(0、1、2、3…)
则小球所在C点距水平面的高度H是
H=
gt02=
(K=0、1、2、3…)
答:小球所在C点距水平面的高度H是
(K=0、1、2、3…).
| 3 |
| 4 |
得到T=
| 4 |
| 3 |
当振子与小球恰好到O点处相碰时,振子运动的时间为t0=
| T |
| 4 |
则小球所在C点距水平面的高度H是
H=
| 1 |
| 2 |
| g(2K+1)2t2 |
| 18 |
答:小球所在C点距水平面的高度H是
| g(2K+1)2t2 |
| 18 |
点评:本题关键要抓住简谐运动的周期性,得到的时间是一个通式,不要简单地认为小球自由下落的时间t0=
,当作特殊值去求,造成漏解.
| T |
| 4 |

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
 如图所示为一弹簧振子做简谐运动的位移图象,由图象可知该弹簧振子的振幅为
如图所示为一弹簧振子做简谐运动的位移图象,由图象可知该弹簧振子的振幅为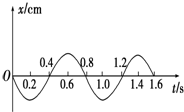 如图所示为一弹簧振子的振动图象,在0~0.8s 时间内,下列说法正确的是( )
如图所示为一弹簧振子的振动图象,在0~0.8s 时间内,下列说法正确的是( ) (2011?静安区二模)如图所示,一弹簧振子在B、C两点间做机械振动,B、C间距为12cm,O是平衡位置,振子每次从C运动到B的时间均为0.5s,则下列说法中正确的是( )
(2011?静安区二模)如图所示,一弹簧振子在B、C两点间做机械振动,B、C间距为12cm,O是平衡位置,振子每次从C运动到B的时间均为0.5s,则下列说法中正确的是( )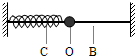 如图所示,一弹簧振子在B、C两点间做机械振动,B、C之间的距离为12cm,O是平衡位置,振子每次从C运动到B的时间均为0.5s,该弹簧振子( )
如图所示,一弹簧振子在B、C两点间做机械振动,B、C之间的距离为12cm,O是平衡位置,振子每次从C运动到B的时间均为0.5s,该弹簧振子( )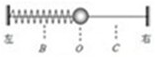 如图所示,一弹簧振子沿光滑水平杆在BC间做简谐运动,O为平衡位置,振幅A=6cm.从振子经过图中B点时开始计时,经时间0.1s第一次到达O点,则振子的振动周期T=
如图所示,一弹簧振子沿光滑水平杆在BC间做简谐运动,O为平衡位置,振幅A=6cm.从振子经过图中B点时开始计时,经时间0.1s第一次到达O点,则振子的振动周期T=