题目内容
【题目】带有 ![]() 光滑圆弧轨道、质量为M的滑车静止置于光滑水平面上,如图所示,一质量为m的小球以速度v0水平冲上滑车,到达某一高度后,小球又返回车的左端.若M=2m,则( )
光滑圆弧轨道、质量为M的滑车静止置于光滑水平面上,如图所示,一质量为m的小球以速度v0水平冲上滑车,到达某一高度后,小球又返回车的左端.若M=2m,则( )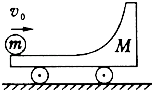
A.小球以后将向左做平抛运动
B.小球将做自由落体运动
C.此过程中小球对小车做的功为 ![]()
D.小球在弧形槽上升的最大高度为 ![]()
【答案】A,C,D
【解析】解:AB、小球滑上滑车,又返回,到离开滑车的整个过程中,系统水平方向动量守恒.选取向右为正方向,由动量守恒定律得:
mv0=mv1+Mv2
由机械能守恒定律得: ![]() mv02=
mv02= ![]() mv12+
mv12+ ![]() Mv22
Mv22
解得:v1= ![]() =﹣
=﹣ ![]() ,
,
v2= ![]() =
= ![]()
所以小球以后将向左做平抛运动,故A正确,B错误.
C、对小车,运用动能定理得:小球对小车做的功 W= ![]() Mv22﹣0=
Mv22﹣0= ![]() ,故C正确.
,故C正确.
D、当小球与小车的速度相同时,小球上升到最大高度,设共同速度为v.规定向右为正方向,运用动量守恒定律得:
mv0=(m+M)v
根据能量守恒定律得,有:
![]() mv02﹣
mv02﹣ ![]() (m+M)v2=mgh
(m+M)v2=mgh
代入数据得:h= ![]() ,故D正确.
,故D正确.
故选:ACD
小球和小车组成的系统,在水平方向上动量守恒,小球越过圆弧轨道后,在水平方向上与小车的速度相同,返回时仍然落回轨道,根据动量守恒定律判断小球的运动情况.对小车,运用动能定理求小球对小车做的功.当小球与小车的速度相同时,小球上升到最大高度,由动量守恒定律和机械能守恒定律结合求解最大高度.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目