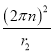Question

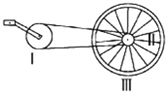
【题目】套着弹簧与小球P的粗糙细杆固定在如图所示的装置上，弹簧的一端固定在装置的A点，另一端连接一质量为m的小球P，当整个装置静止时，弹簧处于压缩状态，小球P离A点的距离为2L，离B点的距离为4L，那么当整个装置绕过AB中点的竖直中心轴OO’以角速度ω匀速转动时，下列说法正确的是（ ）

A. 小球P一定不会更靠近B点 B. 小球P相对B点距离一定变化

C. 小球P受到的弹簧弹力可能为 D. 小球受到的静摩擦力一定变小

Answer 1

【答案】AC

【解析】

当整个装置静止时，弹簧处于拉伸状态，说明小球静止时受向右的摩擦力，当整个装置绕竖直中心轴OO′以角速度ω匀速转动时，小球所受的合力提供向心力．

当整个装置静止时，由平衡条件知小球受向左的摩擦力，此时弹力F=f；当整个装置绕竖直中心轴OO′以角速度ω匀速转动时，小球所受合力由P指向O，由题意知AB之间距离为6L，则OB=3L，则OP=3L-2L=L，因F-f1=mω2L，可知f1<f，则小球P不会有向B靠近的趋势，即不会更靠更靠近B，小球P相对B点距离可能不变，故A正确，B错误；若小球位子不变，小球与杆之间的静摩擦力为零，则圆周运动的半径为L，根据牛顿第二定律小球P受到的合力等于弹簧的弹力，大小为mω2L，故C正确；若小球转动的角速度比较大，则小球需要的向心力较大，可能会受到向右的较大的静摩擦力，故小球受到的静摩擦力不一定变小，故D错误；故选AC。