Question

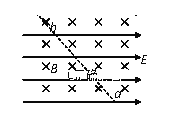
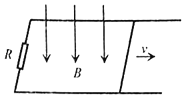
【题目】如图，MN、PQ为足够长的平行金属导轨，间距L=0.2m，导轨平面与水平面间夹角370,N、Q间连接一个电阻R=0.1Ω，匀强磁场垂直于导轨平面向上，磁感应强度B=0.5T，一根质量m=0.03kg的金属棒正在以速度v=1.2m/s的速度沿导轨匀速下滑，下滑过程中始终与导轨垂直，且与导轨接触良好金属棒及导轨的电阻不计，求：

(1)电阻R中电流的大小；

(2)金属棒与导轨间的滑动摩擦因数的大小；

(3)如果从某时刻开始对金属棒施加一个垂直于金属棒且沿导轨平面向上的恒定拉力F=0.2N，金属棒将继续下滑x=0.14m后速度恰好减为0，则在金属棒减速过程中电阻R中产生的焦耳热为多少？

Answer 1

【答案】(1) 1.2A (2) 0.25 (3) 1.04×10-2J

【解析】

（1）根据E=BLv可求得感应电动势，再根据欧姆定律可求得电流大小；
（2）金属棒匀速运动时，受力平衡，分别对沿斜面和垂直斜面根据平衡条件列式，即可求得动摩擦因数；
（3）对全过程进行分析，明确能量关系，根据功能关系即可求得R上产生的热量．

（1）感应电动势E=BLv=0.5×0.2×1.2=0.12V；
感应电流；
（2）导体棒受到的安培力F安=BIL=0.5×0.2×1.2=0.12N；
金属棒匀速下滑，根据平衡条件可知：
mgsinθ-f-F安=0
且FN-mgcosθ=0
又f=μFN
代入数据解得：μ=0.25；
（3）从施加拉力F到金属棒停下的过程中，由能量守恒定律得：
（F-mgsinθ+μmgcosθ）x+Q=mv2
代入数据解得：产生的焦耳热：Q=1.04×10-2J．