题目内容
4.在地面上方的A点以$\sqrt{3}$m/s的初速度水平抛出一个质量为2kg的小球,小球刚落地前的瞬时动能为7J,落地点在B点,不计空气阻力,则A、B两点的连线与水平方向的夹角为30°,落地前瞬时小球重力做功的功率为40W.分析 物体做的是平抛运动,根据水平方向的匀速直线运动和竖直方向上的自由落体运动,求出A、B两点的连线与水平方向的夹角的正切值,即可求得夹角的大小,根据P=mgvcosθ=mgvy求出重力的瞬时功率.
解答 解:设物体的质量为m,物体的动能为E1=$\frac{1}{2}$mv2=$\frac{1}{2}$×2×3=3J,物体的末动能E2=7J,
根据E2=$\frac{1}{2}$mv2=7J,
所以物体的速度v为v=$\sqrt{7}$m/s,
所以物体在竖直方向上的速度的大小为vy=$\sqrt{{v}^{2}{-v}_{0}^{2}}$=2m/s,
设A、B两点的连线与水平方向的夹角为θ,
则tanθ=$\frac{y}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{2{v}_{0}}$=$\frac{{v}_{y}}{2{v}_{0}}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
所以θ=30°,小球落地前竖直分速度vy=gt=2m/s
重力的瞬时功率PG=mg vy=40W.
故答案为:30°,40
点评 本题就是对平抛运动规律的考查,平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动来求解,以及掌握瞬时功率的公式P=Fvcosθ.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
9.下列四张图中,沿MN直线从M到N的过程中,电势一直减小的是( )
| A. |  两个等量异种电荷 | B. | 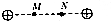 两个等量同种电荷 | ||
| C. | 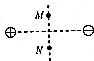 两个等量异种电荷 | D. | 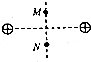 两个等量同种电荷 |

 已知斜面长14m,倾角为30°,物体与斜面间的动摩擦因数为μ,物体至少以多大的初速端沿斜面向上滑,才能使物体到达斜面的顶端?
已知斜面长14m,倾角为30°,物体与斜面间的动摩擦因数为μ,物体至少以多大的初速端沿斜面向上滑,才能使物体到达斜面的顶端? 如图甲所示为某电阻R随摄氏温度t变化的关系图象,图中R0表示0℃时的电阻值,k表示图线的斜率.若用该电阻与电池(电动势为E,内阻为r)、电流表(满偏电流为Ig、内阻为Rg)、滑动变阻器R′串联起来,连接成如图乙所示的电路,用该电阻做测温探头,把电流表的电流刻度改为相应的温度刻度,于是就得到了一个简单的“电阻温度计”.
如图甲所示为某电阻R随摄氏温度t变化的关系图象,图中R0表示0℃时的电阻值,k表示图线的斜率.若用该电阻与电池(电动势为E,内阻为r)、电流表(满偏电流为Ig、内阻为Rg)、滑动变阻器R′串联起来,连接成如图乙所示的电路,用该电阻做测温探头,把电流表的电流刻度改为相应的温度刻度,于是就得到了一个简单的“电阻温度计”.
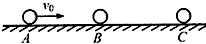 如图所示,在水平光滑直导轨上,静止着三个大小相同小球A、B、C,质量分别为mA=mC=1.0kg,mB=2.0kg,现让A球以v0=3m/s的速度向着B球运动,A、B两球碰撞后粘合在一起,两球继续向右运动并跟C球碰撞,C球的最终动量是系统总动量的$\frac{1}{2}$,求A、B、C球最终的速度大小.
如图所示,在水平光滑直导轨上,静止着三个大小相同小球A、B、C,质量分别为mA=mC=1.0kg,mB=2.0kg,现让A球以v0=3m/s的速度向着B球运动,A、B两球碰撞后粘合在一起,两球继续向右运动并跟C球碰撞,C球的最终动量是系统总动量的$\frac{1}{2}$,求A、B、C球最终的速度大小. 如图所示,质量为m=1kg的可视为质点的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进人竖直固定的光滑圆弧轨道下滑,圆弧轨道与质量为M=2kg的足够长的小车左端在最低点O点相切,并在O点滑上静止在光滑水平地面上的小车,当物块运动到障碍物Q处时与Q发生无机械能损失的碰撞,碰撞前物块和小车已经相对静止,而小车可继续向右运动(物块始终在小车上),小车和物块在运动过程中和圆弧无相互作用.已知圆弧半径R=1.0m,圆弧对应的圆心角θ为53°,A、B两点间的高度差h=0.8m,物块与小车间的动摩擦因数为μ=0.1,重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.试求:
如图所示,质量为m=1kg的可视为质点的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进人竖直固定的光滑圆弧轨道下滑,圆弧轨道与质量为M=2kg的足够长的小车左端在最低点O点相切,并在O点滑上静止在光滑水平地面上的小车,当物块运动到障碍物Q处时与Q发生无机械能损失的碰撞,碰撞前物块和小车已经相对静止,而小车可继续向右运动(物块始终在小车上),小车和物块在运动过程中和圆弧无相互作用.已知圆弧半径R=1.0m,圆弧对应的圆心角θ为53°,A、B两点间的高度差h=0.8m,物块与小车间的动摩擦因数为μ=0.1,重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.试求: