题目内容
19. 如图甲所示为某电阻R随摄氏温度t变化的关系图象,图中R0表示0℃时的电阻值,k表示图线的斜率.若用该电阻与电池(电动势为E,内阻为r)、电流表(满偏电流为Ig、内阻为Rg)、滑动变阻器R′串联起来,连接成如图乙所示的电路,用该电阻做测温探头,把电流表的电流刻度改为相应的温度刻度,于是就得到了一个简单的“电阻温度计”.
如图甲所示为某电阻R随摄氏温度t变化的关系图象,图中R0表示0℃时的电阻值,k表示图线的斜率.若用该电阻与电池(电动势为E,内阻为r)、电流表(满偏电流为Ig、内阻为Rg)、滑动变阻器R′串联起来,连接成如图乙所示的电路,用该电阻做测温探头,把电流表的电流刻度改为相应的温度刻度,于是就得到了一个简单的“电阻温度计”.(1)使用“电阻温度计”前,先要把电流表的刻度改为相应的温度值,若温度t1<t2其对应的电流分别为I1、I2,则I1、I2谁大?
(2)若该“电阻温度计”的最低适用温度为0℃,即当温度为0℃时,电流表恰好达到满偏电流Ig,则变阻器R′的阻值为多大?
(3)若保持(2)中电阻R′的值不变,则电流表刻度为I时所对应的温度t为多大?
(4)将电流表刻度盘换为温度刻度盘,刻度均匀吗?说明理由.
分析 (1)由a图可知温度与电阻的关系;再由闭合电路欧姆定律可得出电流的关系;
(2)由闭合电路欧姆定律可求得变阻器R′的阻值;
(3)由图a电阻与时间的关系,再由闭合电路欧姆定律可得出时间的表达式;
(4)由时间的表达式可知时间与电流的关系,则可知刻度是否均匀.
解答 解:(1)由图(a)可知温度越高,电阻R越大,对应电路中的电流越小,故I1>I2.
(2)由闭合电路欧姆定律得:
Ig=$\frac{E}{r+R+{R}_{g}+{R}_{0}}$
得:R′=$\frac{E}{{I}_{g}}$-R0-Rg-r.
(3)由图(a)得R=R0+kt
再由闭合电路欧姆定律得:
I=$\frac{E}{r+R+{R}_{g}+R′}$
解之得:t=$\frac{E}{k}$($\frac{1}{I}$-$\frac{1}{Ig}$).
(4)由t=$\frac{E}{k}$($\frac{1}{I}$-$\frac{1}{Ig}$)可知t与I不是一次线性关系,故刻度不均匀.
答:(1)使用“电阻温度计”前,先要把电流表的刻度改为相应的温度值,若温度t1<t2其对应的电流分别为I1、I2,则I1>2,
(2)变阻器R′的阻值为$\frac{E}{{I}_{g}}$-R0-Rg-r;
(3)电流表刻度为I时所对应的温度t为$\frac{E}{k}$($\frac{1}{I}$-$\frac{1}{Ig}$);
(4)由t=$\frac{E}{k}$($\frac{1}{I}$-$\frac{1}{Ig}$)可知t与I不是一次线性关系,故刻度不均匀.
点评 本题考查闭合电路欧姆定律,要注意根据图象进行分析,明确题目中给出的信息,再结合闭合电路欧姆定律进行分析即可得出结论.

练习册系列答案
相关题目
9. 如图所示,一电子沿等量异种电荷的中垂线由A→O→B运动,电子重力不计,则电子仅受电场力作用,则电子受力情况是( )
如图所示,一电子沿等量异种电荷的中垂线由A→O→B运动,电子重力不计,则电子仅受电场力作用,则电子受力情况是( )
 如图所示,一电子沿等量异种电荷的中垂线由A→O→B运动,电子重力不计,则电子仅受电场力作用,则电子受力情况是( )
如图所示,一电子沿等量异种电荷的中垂线由A→O→B运动,电子重力不计,则电子仅受电场力作用,则电子受力情况是( )| A. | 先变大后变小,方向水平向左 | B. | 先变大后变小,方向水平向右 | ||
| C. | 先变小后变大,方向水平向左 | D. | 先变小后变大,方向水平向右 |
7.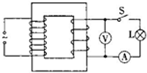 如图所示,理想变压器的原线圈通有e=30$\sqrt{2}$cos100πt(V)的交变电流,灯泡L的额定功率为6W,开关S闭合后灯泡L恰好正常发光,电压表、电流表均为理想电表.变压器的原、副线圈的匝数比为10:1,下列说法正确的是( )
如图所示,理想变压器的原线圈通有e=30$\sqrt{2}$cos100πt(V)的交变电流,灯泡L的额定功率为6W,开关S闭合后灯泡L恰好正常发光,电压表、电流表均为理想电表.变压器的原、副线圈的匝数比为10:1,下列说法正确的是( )
 如图所示,理想变压器的原线圈通有e=30$\sqrt{2}$cos100πt(V)的交变电流,灯泡L的额定功率为6W,开关S闭合后灯泡L恰好正常发光,电压表、电流表均为理想电表.变压器的原、副线圈的匝数比为10:1,下列说法正确的是( )
如图所示,理想变压器的原线圈通有e=30$\sqrt{2}$cos100πt(V)的交变电流,灯泡L的额定功率为6W,开关S闭合后灯泡L恰好正常发光,电压表、电流表均为理想电表.变压器的原、副线圈的匝数比为10:1,下列说法正确的是( )| A. | 副线圈交变电流的频率为5Hz | B. | 电压表的示数为4.24V | ||
| C. | 电流表的示数为0.2A | D. | 灯泡正常发光时的电阻为1.5Ω |
14.一个小物体从固定的斜面顶端匀速下滑,则在下滑的过程中小物体受到力的个数为( )

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.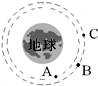 如图所示,A、B、C是地球大气层外圆形轨道上运行的三颗人造地球卫星,A、B质量相同,且大于C的质量,则( )
如图所示,A、B、C是地球大气层外圆形轨道上运行的三颗人造地球卫星,A、B质量相同,且大于C的质量,则( )
 如图所示,A、B、C是地球大气层外圆形轨道上运行的三颗人造地球卫星,A、B质量相同,且大于C的质量,则( )
如图所示,A、B、C是地球大气层外圆形轨道上运行的三颗人造地球卫星,A、B质量相同,且大于C的质量,则( )| A. | A所需向心力最大 | |
| B. | 从图中位置开始A一定先与B相距最近 | |
| C. | B、C向心加速度相等,且小于A的向心加速度 | |
| D. | B、C的线速度大小相等,且大于A的线速度 |
9.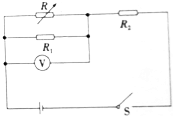 如图所示连接的电路中,闭合开关调节电阻箱,使电压表的示数增大△U,已知电源的内阻不能忽略,用I1、I2分别表示流过R1、R2的电流,△I1、△I2分别表示流过R1、R2的电流的变化量,U1、U2分别表示R1、R2两端的电压,则下列说法正确的是( )
如图所示连接的电路中,闭合开关调节电阻箱,使电压表的示数增大△U,已知电源的内阻不能忽略,用I1、I2分别表示流过R1、R2的电流,△I1、△I2分别表示流过R1、R2的电流的变化量,U1、U2分别表示R1、R2两端的电压,则下列说法正确的是( )
 如图所示连接的电路中,闭合开关调节电阻箱,使电压表的示数增大△U,已知电源的内阻不能忽略,用I1、I2分别表示流过R1、R2的电流,△I1、△I2分别表示流过R1、R2的电流的变化量,U1、U2分别表示R1、R2两端的电压,则下列说法正确的是( )
如图所示连接的电路中,闭合开关调节电阻箱,使电压表的示数增大△U,已知电源的内阻不能忽略,用I1、I2分别表示流过R1、R2的电流,△I1、△I2分别表示流过R1、R2的电流的变化量,U1、U2分别表示R1、R2两端的电压,则下列说法正确的是( )| A. | △I1>0,且△I1=$\frac{△U}{{R}_{1}}$ | |
| B. | U2减小,且△U2=△U | |
| C. | I1减小,且△I2<$\frac{△U}{{R}_{2}}$ | |
| D. | 电源的输出电压增大,且增大量为△U |
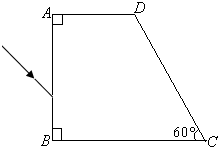 如图所示,为用某种透明材料制成为一块柱体棱镜的水平截面图,角A与角B为直角,角C等于60°,光线从AB边入射,入射角为45°,已知棱镜材料对该光的折射率为$n=\sqrt{2}$
如图所示,为用某种透明材料制成为一块柱体棱镜的水平截面图,角A与角B为直角,角C等于60°,光线从AB边入射,入射角为45°,已知棱镜材料对该光的折射率为$n=\sqrt{2}$ 有一小灯泡上标有“3V 0.3A”字样,现要描绘该小灯泡的伏安特性曲线,有下列器材供选用:
有一小灯泡上标有“3V 0.3A”字样,现要描绘该小灯泡的伏安特性曲线,有下列器材供选用: