题目内容
如图所示,质量为M长方体木板A放在光滑的水平面上,一个质量为m小物体B从长方体木板A的最左端以水平向右的初速度v0沿木板上表面开始运动,假设运动的整个过程中小物体B受到竖直向上的恒力F=
mg的作用,当小物体B滑到木板A的最右端时,小物体与木板恰好相对静止.

(1)若已知木板的长为l,小物体与木板之间的动摩擦因数为μ,当地的重力加速度为g,求木板的质量M与小物体的质量m的比值;
(2)如只将小物体B受到的恒力F大小保持不变,方向变为竖直向下,当小物体B以另一水平向右的初速度v0从木板的最左端开始运动,当小物体滑到木板的最右端时,小物体与木板也恰好相对静止,求
与v0之比.
| 4 |
| 5 |

(1)若已知木板的长为l,小物体与木板之间的动摩擦因数为μ,当地的重力加速度为g,求木板的质量M与小物体的质量m的比值;
(2)如只将小物体B受到的恒力F大小保持不变,方向变为竖直向下,当小物体B以另一水平向右的初速度v0从木板的最左端开始运动,当小物体滑到木板的最右端时,小物体与木板也恰好相对静止,求
| v | ′ 0 |
分析:(1)由两物体的受力可以求得其加速度,由于当小物体B滑到木板A的最右端时,小物体与木板恰好相对静止,故两者末速度相等,列位移关系式,可以解得质量之比.
(2)力F的方向改变,会改变M与m间的摩擦力,进而改变加速度,依据力的改变算出M和m的加速度,代入表达式可以得到速度比值
(2)力F的方向改变,会改变M与m间的摩擦力,进而改变加速度,依据力的改变算出M和m的加速度,代入表达式可以得到速度比值
解答:解:
(1)m竖直方向受重力,支持力N,F三力平衡,故有:mg=N+F,水平方向受摩擦力,由牛顿第二定律:-f=ma1,f=μN=μ(mg-F),
解得:a1=
=
=-0.2μg,对M其水平方向受摩擦力大小为f,方向向右,故其加速度为:a2=
=
,
对m由运动学得:x1=v0t+
a1t2,
对M:x2=
a2t2,由位移关系:x1-x2=l,代入:v0t+
a1t2-
a2t2=l①,
又末速度相等:a2t=v0+a1t
即:t=
②,
解得:
=a2-a1③,
即:
=
+
④,
解得
=
-1
(2)若力F变为向下,对m有N=mg+F,则m的加速度变为:a1′=
=
=-
,
M的加速度变为:a2′=
=
,带入③式得:
=
+
,
解得:v0′=
,
由④解得:v0=
,
故
与v0之比为:
=3:1
答:(1)木板的质量M与小物体的质量m的比值为:
=
-1
(2)
与v0之比为:
=3:1
(1)m竖直方向受重力,支持力N,F三力平衡,故有:mg=N+F,水平方向受摩擦力,由牛顿第二定律:-f=ma1,f=μN=μ(mg-F),
解得:a1=
| -f |
| m |
| -μ(mg-F) |
| m |
| f |
| M |
| μmg |
| 5M |
对m由运动学得:x1=v0t+
| 1 |
| 2 |
对M:x2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又末速度相等:a2t=v0+a1t
即:t=
| v0 |
| a2-a1 |
解得:
| v02 |
| 2l |
即:
| v02 |
| 2l |
| μmg |
| 5M |
| μg |
| 5 |
解得
| m |
| M |
| 5v02 |
| 2μgl |
(2)若力F变为向下,对m有N=mg+F,则m的加速度变为:a1′=
| -f′ |
| m |
| -μ(mg+F) |
| m |
| 9μg |
| 5 |
M的加速度变为:a2′=
| f′ |
| M |
| 9μmg |
| 5M |
| v0′2 |
| 2l |
| 9μmg |
| 5M |
| 9μg |
| 5 |
解得:v0′=
2l(
|
由④解得:v0=
2l(
|
故
| v | ′ 0 |
| v0′ |
| v0 |
答:(1)木板的质量M与小物体的质量m的比值为:
| m |
| M |
| 5v02 |
| 2μgl |
(2)
| v | ′ 0 |
| v0′ |
| v0 |
点评:本题重点要能从位移和速度的关系式变化出质量的比值,主要就是公式的变形处理问题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图所示,质量为m、边长为L的正方形闭合线圈从有理想边界的水平匀强磁场上方h高处由静止下落,磁场区域的边界水平,磁感应强度大小为B.线圈的电阻为R,线圈平面始终在竖直面内并与磁场方面垂直,ab边始终保持水平.若线圈一半进入磁场时恰好开始做匀速运动,重力加速度为g.求:
如图所示,质量为m、边长为L的正方形闭合线圈从有理想边界的水平匀强磁场上方h高处由静止下落,磁场区域的边界水平,磁感应强度大小为B.线圈的电阻为R,线圈平面始终在竖直面内并与磁场方面垂直,ab边始终保持水平.若线圈一半进入磁场时恰好开始做匀速运动,重力加速度为g.求: 如图所示,质量为m的木板静止的放在光滑水平面上,质量为2m、可视为质点的木块以水平速度v0从左端滑上木板.木块与木板间的动摩擦因数为μ,木板足够长.
如图所示,质量为m的木板静止的放在光滑水平面上,质量为2m、可视为质点的木块以水平速度v0从左端滑上木板.木块与木板间的动摩擦因数为μ,木板足够长. 如图所示,质量为M=0.60Kg的小沙箱,被长为L=1.60m的细绳悬于空中某点,现从左向右用枪以v0=10m/s的速度向沙箱发射质量m=0.20Kg的子弹,假设沙箱每次在最低点时,就恰好有一颗子弹射入沙箱,并留在其中.(g=10m/s2,不计空气阻力,子弹与沙箱相互作用时间极短)则:
如图所示,质量为M=0.60Kg的小沙箱,被长为L=1.60m的细绳悬于空中某点,现从左向右用枪以v0=10m/s的速度向沙箱发射质量m=0.20Kg的子弹,假设沙箱每次在最低点时,就恰好有一颗子弹射入沙箱,并留在其中.(g=10m/s2,不计空气阻力,子弹与沙箱相互作用时间极短)则: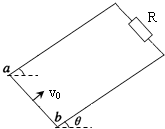 如图所示,质量为m,阻值为R的导体棒ab垂直放在光滑足够长的U形导轨的底端,U形导轨的顶端连接一个阻值为R的电阻,导轨平面与水平面成θ角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,在导体棒上升到最高点的过程中电阻上产生了Q的热量,返回过程中,导体棒在到达底端前已经做匀速运动,速度大小为
如图所示,质量为m,阻值为R的导体棒ab垂直放在光滑足够长的U形导轨的底端,U形导轨的顶端连接一个阻值为R的电阻,导轨平面与水平面成θ角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,在导体棒上升到最高点的过程中电阻上产生了Q的热量,返回过程中,导体棒在到达底端前已经做匀速运动,速度大小为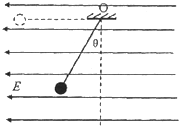 如图所示,质量为m的带电小球用长为L的绝缘细线(不可伸长)悬挂于O点,并处在场强为E、水平向左的匀强电场中,球静止时丝线与竖直方向的夹角为θ=37°.现将小球拉至虚线所示位置(细线水平拉直,与O点相同高度)后从静止开始释放,则:
如图所示,质量为m的带电小球用长为L的绝缘细线(不可伸长)悬挂于O点,并处在场强为E、水平向左的匀强电场中,球静止时丝线与竖直方向的夹角为θ=37°.现将小球拉至虚线所示位置(细线水平拉直,与O点相同高度)后从静止开始释放,则: