题目内容
12. 如图所示,一质量M=990g的木块(不计木块大小)用一长L=0.5m的细线悬挂着处于静止,用气枪水平对准木块射击,已知气枪子弹质量m=10g,若气枪子弹与木块作用时间极短且留在木块中,击中后一起向上摆动,不计空气阻力,细线偏离竖直方向的最大偏角θ=53°,g取10m/s2,cos53°=0.6,试求:
如图所示,一质量M=990g的木块(不计木块大小)用一长L=0.5m的细线悬挂着处于静止,用气枪水平对准木块射击,已知气枪子弹质量m=10g,若气枪子弹与木块作用时间极短且留在木块中,击中后一起向上摆动,不计空气阻力,细线偏离竖直方向的最大偏角θ=53°,g取10m/s2,cos53°=0.6,试求:(1)子弹击中木块后二者瞬间速度大小和此时细线的拉力大小?
(2)子弹射入木块前的速度大小?
(3)子弹击中木块过程中机械能的损失?
(4)若细线能够承受的最大拉力为Fm=28N,为使细线不断,子弹射入的速度不能超过多大?
分析 (1)子弹击中木块一起向上摆动的过程中,根据动能定理求出子弹击中木块后二者瞬间速度大小,在击中瞬间,根据向心力公式求出绳子的拉力;
(2)子弹击中木块的过程中,动量守恒,根据动量守恒定律求出子弹射入木块前的速度大小;
(3)子弹击中木块过程中机械能的损失量等于击中前子弹的动能减去击中后子弹和木块的总动能;
(4)在最低点,根据向心力公式求出子弹和木块的最大速度,再根据动量守恒定律求出子弹的最大速度.
解答 解:(1)子弹击中木块一起向上摆动的过程中,根据动能定理得:
0-$\frac{1}{2}(M+m){v}^{2}=-(M+m)gL(1-cos53°)$
解得:v=2m/s
在击中瞬间,根据向心力公式得:
$T-(m+M)g=(m+M)\frac{{v}^{2}}{L}$
解得:T=18N
(2)子弹击中木块的过程中,动量守恒,根据动量守恒定律得:
mv0=(M+m)v
解得:v0=200m/s
(3)子弹击中木块过程中机械能的损失量$△E=\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}(M-m){v}^{2}=198J$
(4)若细线能够承受的最大拉力为Fm=28N,在最低点,根据向心力公式得:
Fm-(M+m)g=(M+m)$\frac{{{v}_{m}}^{2}}{L}$
解得:vm=3m/s
子弹击中木块的过程中,动量守恒,根据动量守恒定律得:
mv0′=(M+m)vm
解得:v0′=300m/s
即子弹射入的速度不能超过300m/s.
答:(1)子弹击中木块后二者瞬间速度大小为2m/s,此时细线的拉力大小为18N;
(2)子弹射入木块前的速度大小为200m/s;
(3)子弹击中木块过程中机械能的损失为198J;
(4)若细线能够承受的最大拉力为Fm=28N,为使细线不断,子弹射入的速度不能超过300m/s.
点评 本题关键明确子弹射木块过程系统动量守恒,整体摆动过程机械能守恒,在最低点合力提供向心力,注意在子弹击中木块的过程中机械能不守恒,损失的机械能等于击中前子弹的动能减去击中后子弹和木块的总动能,难度适中.

| A. | 整个回路在磁场中运动 | |
| B. | 回路所在处的磁场发生变化 | |
| C. | 穿过回路的磁通量发生变化 | |
| D. | 回路中的一部分导体做切割磁感线运动 |
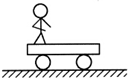 如图所示,光滑的水平地面上有一辆平板车,车上有一个人.原来车和人都静止.当人从左向右行走的过程中( )
如图所示,光滑的水平地面上有一辆平板车,车上有一个人.原来车和人都静止.当人从左向右行走的过程中( )| A. | 人和车组成的系统水平方向动量不守恒 | |
| B. | 人和车组成的系统机械能守恒 | |
| C. | 人和车的速度方向相同 | |
| D. | 人停止行走时,人和车的速度一定均为零 |
| A. | 飞船变轨前后的机械能相等 | |
| B. | 飞船在圆轨道上时航天员出舱前后都处于失重状态 | |
| C. | 飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度 | |
| D. | 飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 |
| A. | α粒子散射实验现象 | B. | 慢中子轰击铀核产生的裂变现象 | ||
| C. | 天然放射现象中的α衰变现象 | D. | 氢原子光谱的特征谱线现象 |
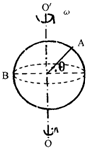 花式篮球是年青人酷爱的一项运动,图示为某同学在单指转篮球,篮球绕中心线OO′匀速转动,A、B为篮球表面不同位置的两点,则( )
花式篮球是年青人酷爱的一项运动,图示为某同学在单指转篮球,篮球绕中心线OO′匀速转动,A、B为篮球表面不同位置的两点,则( )| A. | B点的角速度大于A点角速度 | B. | A、B两点线速度大小相等 | ||
| C. | A、B两点的周期相等 | D. | A、B两点向心加速度大小相等 |
| A. | 光的双缝干涉实验中,若仅将入射光由红光改为紫光,则相邻亮条纹间距一定变大 | |
| B. | 在受迫振动中,驱动力的频率不一定等于物体的固有频率 | |
| C. | 宇航员驾驶宇宙飞船以接近光速经过地球时,地球上的人观察到飞船上的时钟变快 | |
| D. | 光能够发生偏振现象说明光是横波 | |
| E. | 光导纤维传播光信号利用了光的全反射原理 |
 有一柱状透明体,长度为L,其折射率为n1.
有一柱状透明体,长度为L,其折射率为n1.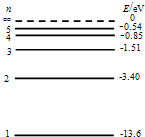 某个光子是氢原子核外电子从n=4跃迁到n=1时所发出的,已知普朗克常量h=6.63×10-34J•s,求:
某个光子是氢原子核外电子从n=4跃迁到n=1时所发出的,已知普朗克常量h=6.63×10-34J•s,求: