题目内容
3. 有一柱状透明体,长度为L,其折射率为n1.
有一柱状透明体,长度为L,其折射率为n1.(1)一光束从左端面垂直于入射,求它在透明体中传播的时间;(真空中的光速为c)
(2)要使从左端任何方向射入的光都能从右端射出,求该透明体的最小折射率n.
分析 (1)由公式v=$\frac{c}{{n}_{1}}$求出光在透明体中传播速度,再由t=$\frac{L}{v}$求出光在透明体中传播的时间.
(2)要使从左端任何方向射入的光都能从右端射出,光线在透明体侧面必须发生全反射,考虑临界情况,即光线在透明体侧面刚好发生全反射的情况,由折射定律和临界角公式结合求解.
解答 解: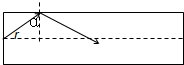 (1)光在透明体中传播速度 v=$\frac{c}{{n}_{1}}$
(1)光在透明体中传播速度 v=$\frac{c}{{n}_{1}}$
则光在透明体中传播的时间 t=$\frac{L}{v}$=$\frac{{n}_{1}L}{c}$
(2)光在左端入射角趋近90°时,光线在透明体侧面刚好发生全反射,此时对应的折射率最小
$\frac{sin90°}{sinr}$=n
由几何关系有 α+r=90°
α=C
又 sinC=$\frac{1}{n}$
解得:n=$\sqrt{2}$
答:
(1)光在透明体中传播的时间为$\frac{{n}_{1}L}{c}$.
(2)该透明体的最小折射率n为$\sqrt{2}$.
点评 本题考查对“光纤通信”原理的理解,关键要掌握全反射的条件,由数学知识求出相关角度的关系.

练习册系列答案
相关题目
13.几位同学想划船渡过一条宽150米的河,他们在静水中划船的速度为5m/s,河水的流速为4m/s,对于这次过河,他们有各自的看法,其中正确的是( )
| A. | 要想到达正对岸就得朝着正对岸划船 | |
| B. | 要想节省时间就得朝着正对岸划船 | |
| C. | 要想位移最小就得朝着正对岸划船 | |
| D. | 船是不可能到达正对岸的 |
8.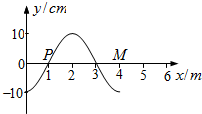 如图所示,一列简谐横波沿x轴正向传播,波传到x=1m的P点时,P点开始向下振动,此时为计时起点,已知在t=0.4s时PM间第一次形成图示波形,此时x=4m的M点正好在波谷.下列说法中正确的是 ( )
如图所示,一列简谐横波沿x轴正向传播,波传到x=1m的P点时,P点开始向下振动,此时为计时起点,已知在t=0.4s时PM间第一次形成图示波形,此时x=4m的M点正好在波谷.下列说法中正确的是 ( )
 如图所示,一列简谐横波沿x轴正向传播,波传到x=1m的P点时,P点开始向下振动,此时为计时起点,已知在t=0.4s时PM间第一次形成图示波形,此时x=4m的M点正好在波谷.下列说法中正确的是 ( )
如图所示,一列简谐横波沿x轴正向传播,波传到x=1m的P点时,P点开始向下振动,此时为计时起点,已知在t=0.4s时PM间第一次形成图示波形,此时x=4m的M点正好在波谷.下列说法中正确的是 ( )| A. | P点的振动周期为0.4s | |
| B. | P点开始振动的方向沿y 轴正方向 | |
| C. | 当M点开始振动时,P点正好在波峰 | |
| D. | 这列波的传播速度是10m/s | |
| E. | 从计时开始的0.4s内,P质点通过的路程为30cm |
15.图甲为远距离输电示意图,升压变压器原副线圈匝数比1:100,降压变压器原副线圈匝数比为100:1,远距离输电线的总电阻为100Ω.若升压变压器的输入电压如图乙所示,输入功率为750kw.下列说法中正确的有( )
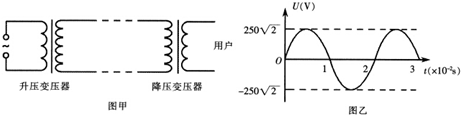

| A. | 客户端交流电的频率为100Hz | B. | 客户端电压为250V | ||
| C. | 输电线中的电流为30A | D. | 输电线路损耗功率为180Kw |
13.某质点做简谐运动,其位移随时间变化的关系式为x=Asin$\frac{π}{4}$t,则质点在( )
| A. | 第1s末与第3s末的位移相同 | B. | 第1s末与第3s末的速度相同 | ||
| C. | 第3s末至第5s末的位移相同 | D. | 第3s末至第5s末的速度相同 |
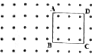 如图所示,正方形线圈ABCD边长为20cm,匝数为200匝,垂直线圈平面的匀强磁场磁感应强度大小为0.1T,如果线圈以AB边为轴,以20πrad/s的角速度匀速转动,则线圈转动过程中,感应电动势的有效值为8$\sqrt{2}$πV,穿过线圈的磁通量变化率最大值为0.08πWb/s.
如图所示,正方形线圈ABCD边长为20cm,匝数为200匝,垂直线圈平面的匀强磁场磁感应强度大小为0.1T,如果线圈以AB边为轴,以20πrad/s的角速度匀速转动,则线圈转动过程中,感应电动势的有效值为8$\sqrt{2}$πV,穿过线圈的磁通量变化率最大值为0.08πWb/s.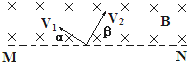 如图所示.直线MN上方垂直纸面向里的、磁感应强度为B的匀强磁场,质量为m、带电量为-q(q>0)的粒子1在纸面内以速度V1=V0从O点射入磁场,其射入方向与MN的夹角α=300;质量为m、带电量为+q(q>0)的粒子2在纸面内以速度V2=$\sqrt{3}$V0也从O点射入磁场,其射入方向与MN的夹角β=60°.已知粒子1和2同时分别到达磁场边界的A、B两点(图中未画出),不计粒子的重力及它们间的相互作用.
如图所示.直线MN上方垂直纸面向里的、磁感应强度为B的匀强磁场,质量为m、带电量为-q(q>0)的粒子1在纸面内以速度V1=V0从O点射入磁场,其射入方向与MN的夹角α=300;质量为m、带电量为+q(q>0)的粒子2在纸面内以速度V2=$\sqrt{3}$V0也从O点射入磁场,其射入方向与MN的夹角β=60°.已知粒子1和2同时分别到达磁场边界的A、B两点(图中未画出),不计粒子的重力及它们间的相互作用.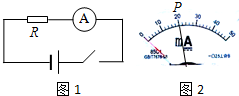 某电阻的阻值R随摄氏温度t的变化情况为R=20+0.2t(Ω),把该电阻与电池、电流表、开关串联起来,电路如图1所示.用该电阻作探头,将电流表的电流刻度改成对应的温度,就做成一简单的电阻温度计.已知电源的电动势为E=2.0V,电流表的最大量程为50mA,它的内阻与电源内阻之和为10Ω.
某电阻的阻值R随摄氏温度t的变化情况为R=20+0.2t(Ω),把该电阻与电池、电流表、开关串联起来,电路如图1所示.用该电阻作探头,将电流表的电流刻度改成对应的温度,就做成一简单的电阻温度计.已知电源的电动势为E=2.0V,电流表的最大量程为50mA,它的内阻与电源内阻之和为10Ω. 如图所示,一质量M=990g的木块(不计木块大小)用一长L=0.5m的细线悬挂着处于静止,用气枪水平对准木块射击,已知气枪子弹质量m=10g,若气枪子弹与木块作用时间极短且留在木块中,击中后一起向上摆动,不计空气阻力,细线偏离竖直方向的最大偏角θ=53°,g取10m/s2,cos53°=0.6,试求:
如图所示,一质量M=990g的木块(不计木块大小)用一长L=0.5m的细线悬挂着处于静止,用气枪水平对准木块射击,已知气枪子弹质量m=10g,若气枪子弹与木块作用时间极短且留在木块中,击中后一起向上摆动,不计空气阻力,细线偏离竖直方向的最大偏角θ=53°,g取10m/s2,cos53°=0.6,试求: