题目内容
（2011?湖南二模）如图甲所示，光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上，两导轨间距L=0.30m．导轨电阻忽略不计，其间连接有固定电阻及=0.40Ω．导轨上停放一质量m=0.10kg、电阻 r=0.20Ω长度也为 L=0.30m的金属杆ab，整个装置处于磁感应强度B=0.50T的匀强磁场中，磁场方向竖直向下．用一外力F沿水平方向拉金属杆ab，使之由静止开始运动，电压传感器可将R两端的电压U即时采集并输入电脑，获得电压U随时间t变化的关系如图乙所示，下列说法中不正确的是（ ）分析：（1）ab棒产生的电动势与v有关，则R两端的电压与v有关，推导出U与v的关系，即可得出v与t的关系，从而可证明金属杆是否做匀加速直线运动以及得出加速度的大小．
（2）根据匀变速直线运动求出2s末的速度，以及在2s末金属杆所受的安培力，根据牛顿第二定律求出拉力，从而求出拉力的瞬时功率．
（3）根据能量守恒定律，拉力做的功全部转化为动能的增加量和整个电路产生的热量．而金属杆上产生的热量与整个电路产生的热量具有这样的关系
=
．
（2）根据匀变速直线运动求出2s末的速度，以及在2s末金属杆所受的安培力，根据牛顿第二定律求出拉力，从而求出拉力的瞬时功率．
（3）根据能量守恒定律，拉力做的功全部转化为动能的增加量和整个电路产生的热量．而金属杆上产生的热量与整个电路产生的热量具有这样的关系
| Q杆 |
| Q |
| r |
| r+R |
解答：解：A、设路端电压为U，金属杆的运动速度为v，则感应电动势E=BLv
电阻R两端的电压U=IR=
由图乙可得U=kt，k=0.1V/s
解得v=
因为速度与时间成正比，所以金属杆做匀加速运动，加速度a=
=1m/s2
故A正确．
B、在2s末，速度v2=at=2m/s
此时通过金属杆的电流I=
金属杆受安培力F安=BIL=0.075N
设2s末外力大小为F2，由牛顿第二定律：F2-F安=ma
故4s末时外力F的瞬时功率 P=F2v2
P=0.35W
故第2s末外力F的瞬时功率为0.35W．故B正确．
C、在2s末，杆的动能Ek=
mv2=0.2J
由能量守恒定律，回路产生的焦耳热：
Q=W-Ek=0.35-0.2=0.15J
又
=
．
故在金属杆上产生的焦耳热Qr=0.05J．故C错误，D正确．
本题选不正确的，故选C．
电阻R两端的电压U=IR=
| BLvR |
| R+r |
由图乙可得U=kt，k=0.1V/s
解得v=
| kt(R+r) |
| BLR |
因为速度与时间成正比，所以金属杆做匀加速运动，加速度a=
| k(R+r) |
| BLR |
故A正确．
B、在2s末，速度v2=at=2m/s
此时通过金属杆的电流I=
| E |
| R+r |
金属杆受安培力F安=BIL=0.075N
设2s末外力大小为F2，由牛顿第二定律：F2-F安=ma
故4s末时外力F的瞬时功率 P=F2v2
P=0.35W
故第2s末外力F的瞬时功率为0.35W．故B正确．
C、在2s末，杆的动能Ek=
| 1 |
| 2 |
由能量守恒定律，回路产生的焦耳热：
Q=W-Ek=0.35-0.2=0.15J
又
| Q杆 |
| Q |
| r |
| r+R |
故在金属杆上产生的焦耳热Qr=0.05J．故C错误，D正确．
本题选不正确的，故选C．
点评：解决本题的关键根据U与t的关系，推导出v与t的关系，掌握导体切割产生的感应电动势大小，以及掌握能量守恒定律．
练习册系列答案
相关题目
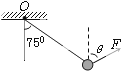（2011?湖南二模）如图所示，一小球用轻绳悬于?点，用力F拉住小球，使悬线保持偏离竖直方向75°角，且小球始终处于平衡状态，为了使F有最小值，F与竖直方向的夹角θ应该是（ ）
（2011?湖南二模）金华到衢州动车共3趟，每趟运行时间约30分钟．把动力装置分散安装在每节车厢上，使其既具有牵引动力，又可以载客，这样的客车车辆叫做动车．而动车组就是几节自带动力的车辆（动车）加几节不带动力的车辆（也叫拖车）编成一组，就是动车组，如图所示．假设动车组运行过程中受到的阻力与其所受重力成正比，每节动车与拖车的质量都相等，每节动车的额定功率都相等．