��Ŀ����
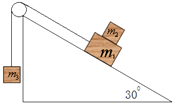
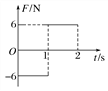
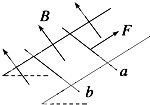
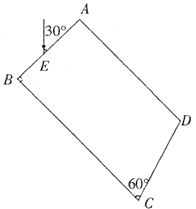
����Ŀ����ͼ����ʾ�����d�������㹻���Ľ����Ƴɵĵ��죬ˮƽ�������ef������һ��ֵΪ2R�Ķ�ֵ���裬���õ�ѹ������ʵ�ʼ�����˵�ѹ����б������ˮƽ��н�Ϊ37�㣮����ҲΪd������Ϊm�Ľ�����ab����ΪR��ͨ���̶��ڰ����˵Ľ����Ử�����ڵ����ϣ������뵼����MG��NH�ζ�Ħ��������= ![]() �����ಿ��Ħ�����ƣ���MN��PQ��GH���ΪL��MN��PQGH���ΪL��MN��PQ���д�ֱ���ƽ�����¡��Ÿ�Ӧǿ��ΪB1����ǿ�ų���PQ��GH����ƽ����б�浫��С������δ֪����ǿ�ų�B2 �� ���������ų���������������ֵ���裬�����������ƣ�sin37��=0.6��cos37��=0.8����ab����MN�Ϸ�һ�������ɾ�ֹ�ͷ�ͨ��MN��QP�����˶�����ab��ʼ�ձ���ˮƽ������ѹ��������U��t��ϵ��ͼ����ʾ��
�����ಿ��Ħ�����ƣ���MN��PQ��GH���ΪL��MN��PQGH���ΪL��MN��PQ���д�ֱ���ƽ�����¡��Ÿ�Ӧǿ��ΪB1����ǿ�ų���PQ��GH����ƽ����б�浫��С������δ֪����ǿ�ų�B2 �� ���������ų���������������ֵ���裬�����������ƣ�sin37��=0.6��cos37��=0.8����ab����MN�Ϸ�һ�������ɾ�ֹ�ͷ�ͨ��MN��QP�����˶�����ab��ʼ�ձ���ˮƽ������ѹ��������U��t��ϵ��ͼ����ʾ��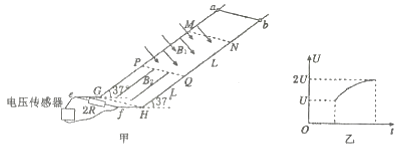
��1����ab���ս���ų�B1ʱ���ٶȴ�С��
��2����ֵ�����ϲ���������Q1��
��3����β������֣���ab����MN��ijһ�ض��ٶȽ���MNQP�����ͬʱ����һ����Ϊ2m������Ϊ2R�Ľ�����cdֻҪ�Եȴ��ٶȴ�PQ����PQHG��������������ͬʱͨ�����Գ���������B2�Ĵ�С�ͷ���
���𰸡�
��1���⣺����ab���ս���ų�B1ʱ��ѹ��������ʾ��ΪU�ɵô�ʱ�ĸ�Ӧ�綯��E1=U+ ![]() =1.5U��
=1.5U��
���ݵ����и�Ÿ��߲����ĸ�Ӧ�綯�Ƽ��㹫ʽ�ɵã�E1=B1dv1
��ã�v1= ![]() ��
��
��ab���ս���ų�B1ʱ���ٶȴ�СΪ ![]() ��
��
��2���⣺�������ab�뿪PQʱ���ٶ�Ϊv2������ͼ�ҿ�֪����ֵ�������˵�ѹΪ2U��
���ݱպϵ�·��ŷķ���ɿɵã� ![]() ��
��
��ã�v2= ![]() ��
��
��ab��MN��PQ�����ݶ��ܶ����ɵã�
mgsin37��L����mgcos37��L��W��= ![]()
���ݹ��ܹ�ϵ�ɵò������ܵĽ�����Q��=W����
���ݽ������ɿɵö�ֵ��������Ľ�����ΪQ1= ![]()
�������Q1= ![]() ��
��
�𣺶�ֵ�����ϲ���������Ϊ ![]()
��3���⣺��������ͬ�ij��ٶȽ��볡�������پ�����ͬ��λ�ƣ���ab�������ݹ�������ƽ��ɵã�
mgsin37�㩁��mgcos37�㩁 ![]() =0��
=0��
��ã�v= ![]() ��
��
��cd������Ϊ2mgsin37�㩁��2mgcos37�㣾0����cd�����������봹ֱ����ƽ�����£�
�������ֶ����֪�Ÿ�Ӧǿ��B2�ص���ƽ�����ϣ�cd��Ҳ�����˶������У�
![]() ��
��
��v= ![]() �����ã�B2=32B1��
�����ã�B2=32B1��
��B2�Ĵ�СΪ32B1�������ص���ƽ������
����������1�����ݵ�ѹ��������ʾ������Ӧ�綯�ƣ����ݵ����и�Ÿ��߲����ĸ�Ӧ�綯�Ƽ��㹫ʽ����ٶȴ�С����2������ͼ�ҿɵ�ab�������˶�ʱ��ֵ�������˵�ѹ�����ݱպϵ�·��ŷķ���ɺͷ����ڵ�Ÿ�Ӧ��������ٶȴ�С�����ݶ��ܶ����������������������ݽ������ɿɵö�ֵ��������Ľ����ȣ���3����������ͬ�ij��ٶȽ��볡�������پ�����ͬ��λ�ƣ��ֱ�Զ�ab����cd�����ݹ�����ƽ�������з������B2���������ֶ����ж�B2����
�����㾫����������Ҫ�����˹��ܹ�ϵ�Ͷ��ܶ������ۺ�Ӧ�õ����֪ʶ�㣬��Ҫ���յ�ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1��Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ�����ȷ�����⣮

����Ŀ���±��г���ijƷ�Ƶ綯���г�����ͼ�������õ綯������Ҫ����������������������е��ģ����ó��ڶ״̬������������ٶ���ʻ���� ��
���� | 40��kg�� | ���ѹ | 48��V�� |
���� | 75��kg�� | ����� | 12��A�� |
�����ʻ�ٶ� | 20��km/h�� | �������� | 350��W�� |

A.�綯�������빦��Ϊ576 W
B.�綯�����ڵ���Ϊ4��
C.�ó��ܵ�������Ϊ63 N
D.�ó���õ�ǣ����Ϊ104 N