题目内容
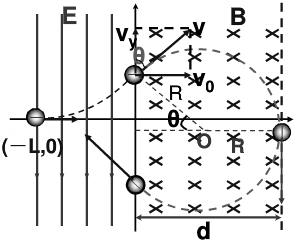
（18分）如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，Y轴为两种场的分界面，图中虚线为磁场区域的右边界，现有一质量为m，电荷量为-q的带电粒子从电场中坐标位置(-L，0)处，以初速度v0沿x轴正方向开始运动，且已知 L=mv02/Eq(重力不计)，试求：
使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d 应满足的条件．
使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d 应满足的条件．
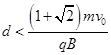
试题分析：粒子在电场中受到的电场力的方向向上，粒子做类平抛运动，水平方向做的是匀速运动，竖直方向做的是匀加速直线运动，设运动的加速度为a．由牛顿运动定律得:qE = ma．
设粒子出电场、入磁场时速度的大小为v，此时在Y轴方向的分速度为vy，粒子在电场中运动的时间为t，速度方向与y轴的夹角为θ，粒子的运动轨迹如图所示，则：
则有:
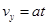
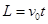
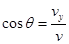
解得：
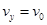
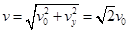
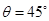
粒子进入磁场后在洛伦兹力作用下做圆周运动，由牛顿第二定律得：
解得：
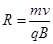
当磁场的运动的轨迹恰好与磁场的右边沿相切时，此时的磁场的宽度最大，根据粒子的运动的轨迹可以知要使粒子穿越磁场区域，磁场的宽度应满足的条件
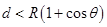
结合已知条件解以上各式可得:
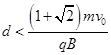
故要使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d应满足的条件为
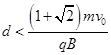
练习册系列答案
相关题目
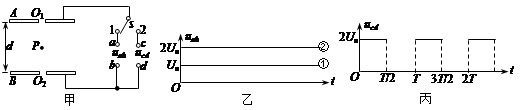
，粒子的重力和粒子之间的作用力均可忽略不计。若某时刻粒子源放出的粒子恰能从平行金属板右边缘离开电场（设在每个粒子通过电场区域的时间内，可以把板间的电场看作是恒定的），同时进入金属板右方磁感强度为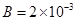
T，方向垂直纸面向里的匀强磁场中，一段时间后正粒子垂直打在屏PQ上，屏PQ与金属板右边缘的距离为d=0.5m。
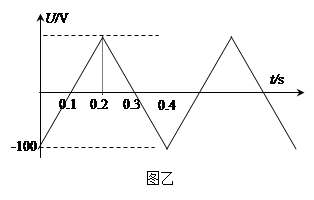
、半径为
的内壁光滑的
圆弧固定轨道，右端通过导线接有阻值为
的电阻，圆弧轨道处于竖直向上的匀强磁场中，磁场的磁感应强度为
。质量为
、电阻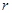为
、长度也为
处由静止开始下滑，到达底端
时，对轨道的压力恰好等于金属棒的重力2倍，不计导轨和导线的电阻，空气阻力忽略不计，重力加速度为
。求：
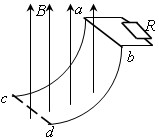
多大；
；
从轨道的低端
。
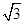倍。将珠子从环最低位置A点静止释放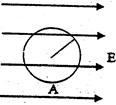，求：
”形导轨PONQ，其质量为M=2.0kg，放在光滑绝缘的水平面上，处于匀强磁场中，另有一根质量为m=0.60kg的金属棒CD跨放在导轨上，CD与导轨的动摩擦因数是0.20，CD棒与ON边平行，左边靠着光滑的固定立柱a、b，匀强磁场以ab为界，左侧的磁场方向竖直向上（图中表示为垂直于纸面向外），右侧磁场方向水平向右，磁感应强度的大小都是0.80T，如图所示，已知导轨ON段长为0.50m，电阻是0.40Ω，金属棒CD的电阻是0.20Ω，其余电阻不计。导轨在水平拉力作用下由静止开始以0.20m/s2的加速度做匀加速直线运动，一直到CD中的电流达到4.0A时，导轨改做匀速直线运动.设导轨足够长，取g=10m/s2.求：
