题目内容
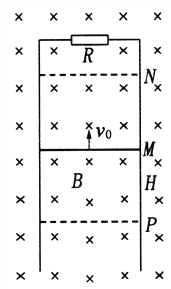
【题目】如图所示,足够长的光滑平行金属导轨竖直放置,间距为L,其上端连接有阻值为R的电阻,装置区域有垂直于导轨平面的匀强磁场,磁感应强度为B。将一根水平金属棒从导轨M处以初速度v0向上抛出,经过时间![]() 到达最高处N,之后下落到P处后速度不再增加,P位于M下方H处。已知金属棒的质量为m,电阻也为R。金属棒在运动中始终保持水平且与导轨良好接触,忽略导轨电阻,重力加速度为g。求:
到达最高处N,之后下落到P处后速度不再增加,P位于M下方H处。已知金属棒的质量为m,电阻也为R。金属棒在运动中始终保持水平且与导轨良好接触,忽略导轨电阻,重力加速度为g。求:
(1)金属棒下落到P处后的速度大小;
(2)金属棒运动过程中最大加速度;
(3)金属棒从N下落到P过程中产生的电能。
【答案】(1)![]() (2)
(2) ![]() (3)
(3)![]()
【解析】(1)金属棒下落到P点后的速度不再增大,说明其加速度为零,由平衡条件知道:
mg-F安=0
而F安=BIL
![]()
E=BLv
整理解得:![]()
(2)经分析可知,金属棒刚向上抛出时加速度最大,由牛顿第二定律:mg+F安=mam
联立解得![]()
(3)设N与M之间的高度差为h,则此上升的过程中,根据动量定理![]() 而
而![]()
![]()
![]()
φ=BhL
整理得:![]()
金属棒从N到P过程中,由能量守恒定律,电路中产生的电能:![]()
整理解得:![]()

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目