题目内容
Ⅰ.某同学要探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L,弹簧下端每增加一个50g的砝码时,指针示数分别记作L1、L2、…、L7.(1)下表记录的是该同学测出的8个值:
| 代表符号 | L | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 6.85 | 8.60 | 10.30 | 12.10 | 14.05 |
(2)根据以上数据,求出弹簧的劲度系数k=______N/m.(g取9.8m/s2)
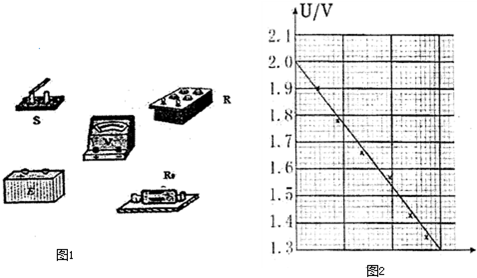
Ⅱ.现要测量某电源的电动势和内阻,备有以下器材:
电源E(电动势小于3V,内阻小于1Ω,最大允许电流1A)
电压表V (量程3V的理想电压表)
电阻箱R(调节范围0-99.99Ω,)
定值电阻R (阻值等于2.00Ω)
导线若干,电键S个
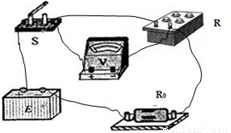
(1)将图1所示的实物连接成实验电路.
(2)闭合开关,调节电阻箱的阻值R.读出电压表相应的示数U,如下图所示,为了比较
准确方便的得出实验结论,现用作图法处理数据,图线纵坐标表示电压表读数U,则图线的横坐标应选用______.
A.R B.
 C.
C. D.
D.
| R/Ω | 40.00 | 20.00 | 12.00 | 8.00 | 6.00 | 5.00 |
| U/V | 1.90 | 1.78 | 1.66 | 1.57 | 1.43 | 1.35 |

Ⅲ.如图a是研究小球在斜面上平抛运动的实验装置,每次将小球从弧型轨道同一位置静止释放,并逐渐改变斜面与水平地面之间的夹角θ,获得不同的射程x,最后作出了如图b所示的x-tanθ图象.则:

(1)由图b可知,小球在斜面顶端水平抛出时的初速度为______;
(2)若最后得到的图象如图c所示,则可能的原因是(写出一个)______.
【答案】分析:Ⅰ.(1)根据d1=L4-L,…,d4=L7-L3,然后通过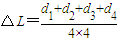 求出每增加50g砝码时弹簧平均伸长量.
求出每增加50g砝码时弹簧平均伸长量.
(2)根据胡克定律求出弹簧的劲度系数.
Ⅱ.本题采用伏阻法测量电源的电动势和内电阻,电压表读数与电阻箱的电阻的比值表示干路中的电流,将定值电阻R 等效到电源的内部,通过U-I图线得出电压的电动势和内阻,注意图线求出的斜率不表示内阻,是电源内阻和定值电阻之和.
Ⅲ.平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,抓住平抛运动竖直位移和水平位移的关系求出运动的时间,从而得出水平位移与tanθ的关系.
解答:解:(1)根据“逐差法”求解,有d1=L4-L,…,d4=L7-L3,故每增加50g砝码的弹簧平均伸长量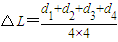 .解得△L=1.75cm;
.解得△L=1.75cm;
(2)由可得: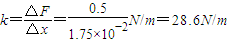 .
.
Ⅱ.(1)本题采用伏阻法测量电源的电动势和内阻,实物图连线如下图.
(2)本题采用伏阻法测量电动势和内阻,图象的纵坐标为路端电压,横坐标为干路电流在本题中即为: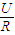 ,故C正确,A、B、D错误.
,故C正确,A、B、D错误.
故选C.
(3)将定值电阻R 等效到电源的内部,电源电动势可以由图中纵轴截距直接读出E=2.0V,横轴坐标为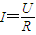 ,每一大格代表0.1A,则图线的斜率
,每一大格代表0.1A,则图线的斜率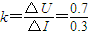 =2.33Ω,所以电源的内阻r=2.33-2=0.33Ω.
=2.33Ω,所以电源的内阻r=2.33-2=0.33Ω.
Ⅲ.每次将小球从弧型轨道同一位置静止释放,知平抛运动的初速度相等,有:tanθ=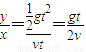 .
.
解得t=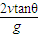 .
.
则x=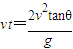 .当tanθ=0.5时,x=0.1m,解得v=1m/s.
.当tanθ=0.5时,x=0.1m,解得v=1m/s.
x=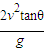 ,知x与tanθ成正比.若出现图C图线,即x比预期的大,可能初速度变大,原因是释放的高度变高.
,知x与tanθ成正比.若出现图C图线,即x比预期的大,可能初速度变大,原因是释放的高度变高.
故答案为:Ⅰ.(1)1.75 (2)28.6
Ⅱ.(1)如图
(2)C (3)2.0; 0.33
Ⅲ.(1)1m/s,(2)释放的高度变高.
点评:本题考查了两个力学实验和一个电学实验,关键掌握实验的原理,掌握图象分析问题的方法.
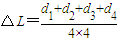 求出每增加50g砝码时弹簧平均伸长量.
求出每增加50g砝码时弹簧平均伸长量.(2)根据胡克定律求出弹簧的劲度系数.
Ⅱ.本题采用伏阻法测量电源的电动势和内电阻,电压表读数与电阻箱的电阻的比值表示干路中的电流,将定值电阻R 等效到电源的内部,通过U-I图线得出电压的电动势和内阻,注意图线求出的斜率不表示内阻,是电源内阻和定值电阻之和.
Ⅲ.平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,抓住平抛运动竖直位移和水平位移的关系求出运动的时间,从而得出水平位移与tanθ的关系.
解答:解:(1)根据“逐差法”求解,有d1=L4-L,…,d4=L7-L3,故每增加50g砝码的弹簧平均伸长量
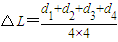 .解得△L=1.75cm;
.解得△L=1.75cm;(2)由可得:
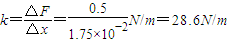 .
.Ⅱ.(1)本题采用伏阻法测量电源的电动势和内阻,实物图连线如下图.
(2)本题采用伏阻法测量电动势和内阻,图象的纵坐标为路端电压,横坐标为干路电流在本题中即为:
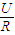 ,故C正确,A、B、D错误.
,故C正确,A、B、D错误.故选C.
(3)将定值电阻R 等效到电源的内部,电源电动势可以由图中纵轴截距直接读出E=2.0V,横轴坐标为
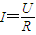 ,每一大格代表0.1A,则图线的斜率
,每一大格代表0.1A,则图线的斜率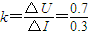 =2.33Ω,所以电源的内阻r=2.33-2=0.33Ω.
=2.33Ω,所以电源的内阻r=2.33-2=0.33Ω.Ⅲ.每次将小球从弧型轨道同一位置静止释放,知平抛运动的初速度相等,有:tanθ=
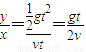 .
.解得t=
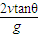 .
.则x=
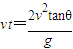 .当tanθ=0.5时,x=0.1m,解得v=1m/s.
.当tanθ=0.5时,x=0.1m,解得v=1m/s.x=
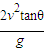 ,知x与tanθ成正比.若出现图C图线,即x比预期的大,可能初速度变大,原因是释放的高度变高.
,知x与tanθ成正比.若出现图C图线,即x比预期的大,可能初速度变大,原因是释放的高度变高.故答案为:Ⅰ.(1)1.75 (2)28.6
Ⅱ.(1)如图

(2)C (3)2.0; 0.33
Ⅲ.(1)1m/s,(2)释放的高度变高.
点评:本题考查了两个力学实验和一个电学实验,关键掌握实验的原理,掌握图象分析问题的方法.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
某同学要探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k。做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上。当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端每增加一个50g的砝码时,指针示数分别记作L1、L2、……、L7。
(1)下表记录的是该同学测出的8个值:
| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 6.85 | 8.60 | 10.30 | 12.10 | 14.05 |
根据表中数据,用“逐差法”计算出每增加50g砝码时弹簧平均伸长量![]() 的数值为
的数值为![]() =___________ cm
=___________ cm
(2)根据以上数据,求出弹簧的劲度系数k= N/m。(g取9.8m/s2)
某同学要探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k。做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上。当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端每增加一个50g的砝码时,指针示数分别记作L1、L2、……、L7。
1.下表记录的是该同学测出的8个值:
|
代表符号 |
L0 |
L1 |
L2 |
L3 |
L4 |
L5 |
L6 |
L7 |
|
刻度数值/cm |
1.70 |
3.40 |
5.10 |
6.85 |
8.60 |
10.30 |
12.10 |
14.05 |
根据表中数据,用“逐差法”计算出每增加50g砝码时弹簧平均伸长量ΔL的数值为ΔL= cm。
2.根据以上数据,求出弹簧的劲度系数k= N/m。(g取9.8m/s2)