题目内容
17．如图，水平的木板B托着木块A一起在竖直平面内沿逆时针方向做匀速圆周运动，下列说法正确的是（ ）
| A． | 物块始终受到三个力作用 | |
| B． | 只有在a、b、c、d四点，物块受到合外力才指向圆心 | |
| C． | 从a到b，物体所受的摩擦力先增大后减小 | |
| D． | 从b到a，物块处于超重状态 |
分析 木板托着物体在竖直平面内逆时针方向一起做匀速圆周运动，物体所受的合力提供圆周运动所需的向心力．当加速度方向向上时，物体处于超重状态，加速度向下时，物体处于失重状态．
解答 解：A、在cd两点处，只受重力和支持力，在其他位置处物体受到重力，支持力、静摩擦力三个作用，故A错误；
B、物体作匀速圆周运动，合外力提供向心力，所以合外力始终指向圆心，故B错误；
C、从a运动到b，物体的加速度的方向始终指向圆心，水平方向的加速度先减小后反向增大，根据牛顿第二定律可得，物体所受木板的摩擦力先减小后增大．故C错误．
D、从b运动到a，向心加速度有向上的分量，所以物体处于超重状态，故D正确；
故选：D
点评 解决本题的关键知道A所受的合力提供向心力，向心力大小不变，知道A所受合力在竖直方向的分力等于重力和支持力的合力，在水平方向的分力等于摩擦力．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
中央电视台推出过一个游戏节目--推矿泉水瓶．选手们从起点开始用力推瓶一段时间后，放手让瓶向前滑动，若瓶最后停在桌上有效区域内，视为成功；若瓶最后不停在有效区域内或在滑行过程中倒下均视为失败．其简化模型如图所示，AC是长度为L1=6m的水平桌面，选手们可将瓶子放在A点，从A点开始用一恒定不变的水平推力推瓶，BC为有效区域．已知BC长度为L2=1m，瓶子质量为m=0.5kg，瓶子与桌面间的动摩擦因数μ=0.5．某选手作用在瓶子上的水平推力F=7.5N，瓶子沿AC做直线运动，g取10m/s2，假设瓶子可视为质点．试通过计算说明：
5．关于公式$\frac{{R}^{3}}{{T}^{2}}$=k，下列说法中正确的是（ ）
| A． | 公式只适用于围绕太阳运行的行星 | |
| B． | 不同星球的行星或卫星，k值均相等 | |
| C． | 围绕同一星球运行的行星或卫星，k值不相等 | |
| D． | 围绕同一星球运行的行星或卫星，k值相等 |
有一面积为S=100cm2金属环，电阻为R=1Ω，环中磁场变化规律如图所示，且磁场方向垂直环面向里，在t1到t2时间内，
2．下列那个核反应方程是重核裂变的方程（ ）
| A． | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n | |
| B． | ${\;}_{15}^{30}$P→${\;}_{14}^{30}$Si+${\;}_{1}^{0}$e | |
| C． | ${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H | |
| D． | ${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{38}^{90}$Sr+${\;}_{54}^{136}$Xe+10${\;}_{0}^{1}$n |
9．在x=-0.5m处有一波源，产生沿x轴正方向传播的简谐横波，传到坐标原点时的波形如图所示．当此波到达P点时，处于原点的O处的质点所通过的路程和该时刻的位移分别是（ ）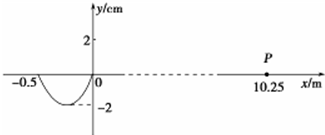
| A． | 10.25 m，2 cm | B． | 10.25 m，-2 cm | C． | 82 cm，-2 cm | D． | 82 cm，2 cm |
6．
在倾角为θ的斜面上固定两根足够长且间距为L的光滑平行金属导轨PQ、MN，导轨处于磁感应强度为B的匀强磁场中，磁场方向垂直于斜面向下．有两根质量分别为m1和m2的金属棒a、b，先将a棒垂直于导轨放置，用跨过光滑定滑轮的细线与物块c连接，连接a棒的细线平行于导轨，由静止释放c，此后某时刻，将b也垂直于导轨放置，此刻起a、c做匀速运动而b静止，a棒在运动过程中始终与导轨垂直，两棒与导轨电接触良好，导轨电阻不计，则（ ）
在倾角为θ的斜面上固定两根足够长且间距为L的光滑平行金属导轨PQ、MN，导轨处于磁感应强度为B的匀强磁场中，磁场方向垂直于斜面向下．有两根质量分别为m1和m2的金属棒a、b，先将a棒垂直于导轨放置，用跨过光滑定滑轮的细线与物块c连接，连接a棒的细线平行于导轨，由静止释放c，此后某时刻，将b也垂直于导轨放置，此刻起a、c做匀速运动而b静止，a棒在运动过程中始终与导轨垂直，两棒与导轨电接触良好，导轨电阻不计，则（ ）| A． | 物块c的质量是（m1+m2）sinθ | |
| B． | b棒放上导轨前，物块c减少的重力势能等于a、c增加的动能 | |
| C． | b棒放上导轨后，a棒克服安培力所做的功等于a棒上消耗的电能 | |
| D． | b棒放上导轨后，b棒中电流大小是$\frac{{m}_{1}gsinθ}{BL}$ |
2．
如图所示，用材料、粗细相同的金属导线制成两个正方形线框Ⅰ和Ⅱ，Ⅰ线框的边长是Ⅱ线框边长的2倍，现将它们置于匀强磁场的边界，分别用力F1、F2把线框Ⅰ和Ⅱ匀速拉进磁场，运动过程中线框平面始终与磁场方向垂直．如果拉力的功率相同，在线框拉进磁场的过程中有（ ）
如图所示，用材料、粗细相同的金属导线制成两个正方形线框Ⅰ和Ⅱ，Ⅰ线框的边长是Ⅱ线框边长的2倍，现将它们置于匀强磁场的边界，分别用力F1、F2把线框Ⅰ和Ⅱ匀速拉进磁场，运动过程中线框平面始终与磁场方向垂直．如果拉力的功率相同，在线框拉进磁场的过程中有（ ）| A． | 线框Ⅰ的感应电动势比线框Ⅱ的感应电动势大 | |
| B． | 线框Ⅰ的感应电流比线框Ⅱ的感应电流大 | |
| C． | 线框Ⅰ的运动速度比线框Ⅱ的运动速度大 | |
| D． | 线框Ⅰ的拉力F1比线框Ⅱ的拉力F2大 |