题目内容
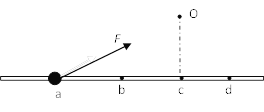
【题目】(17分)如图,在光滑的水平长轨道上,质量为m的小球P1和质量M的小球P2分别置于A、C两点,从某时刻起,P1始终受到向右的大小恒定为F的力作用而向右运动,到C点时与P2发生水平对心正碰（碰撞时间很短,可忽略不计）,碰后瞬间P1速度变为零.已知AC、BC间距离分别为LAC=2L，LCB=L，M=3m.试求：
(1)碰后瞬间P2的速度大小;
（2）两球第二次碰撞前的最大距离dm .
【答案】（1）
（2）
【解析】
试题分析：(1)P1从A到C过程中，由动能定理得：
（2分）
解得：
（1分）
两球碰撞过程内力远大于外力，系统动量守恒，以P1的初速度方向为正方向，
由动量守恒定律得：
(2分)
解得： （2分）
(2)P1做初速度为零的匀加速运动，P2做匀速直线运动，当两者速度相等时，两球间的距离最大，
对P1由牛顿第二定律得：
（1分）
P1的速度：v1=at （1分）
当两球的速度相等时，两球间的距离最大，v1=v （2分）
P1的位移：
（1分）
P2的位移：x2=vt （1分）
两球间的最大距离：
（2分）
解得： （2分）
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
