题目内容
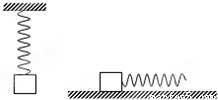
质量为m=4kg的物体在水平轨道上向右运动，当物体的速度v0=15.5m/s时，对物体施加关于初速度反方向对称的两个方向向分别向左下方和右下方（从左向右看）的恒力F1、F2的作用，恒力的大小均为F=25N，恒力的方向与水平面成37°，且两恒力间夹角为120°．如图所示．已知物体与轨道之间的动摩擦因数为0.2，取重力加速度g=10m/s2，求：（1）在此后物体向右运动的最大距离．
（2）6s末时力F2的功率P2． （cos37°=0.8sin37°=0.6）
分析：（1）物体向右做匀减速直线运动，对物体进行受力分析，根据牛顿第二定律及运动学基本公式即可求解；
（2）根据牛顿第二定律求出向左运动的加速度，根据速度时间公式求出6s末时物体的速度，再根据瞬时功率的公式即可求解．
（2）根据牛顿第二定律求出向左运动的加速度，根据速度时间公式求出6s末时物体的速度，再根据瞬时功率的公式即可求解．
解答：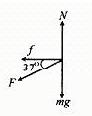
解：（1）物体向右做匀减速直线运动，受力如图所示，设此过程中物体的加速度为a，根据牛顿第二定律有：
2Fcos60°cos37°+f=ma1
N=mg+2Fcos60°sin37°=55N
又因为f=μN
联立方程解得：a1=
代入数据解得：a=7.75m/s2
物体向右运动的最远距离为：s=
=15.5m
（2）物体向左运动时间t2=t-t1=4s
加速度a=
=2.25m/s2
6s末时物体的速度v=a2t2=9m/s
力F2的功率P2=F2vcos600cos370=90W
答：（1）在此后物体向右运动的最大距离为15.5m．
（2）6s末时力F2的功率P2为 90W；．
解：（1）物体向右做匀减速直线运动，受力如图所示，设此过程中物体的加速度为a，根据牛顿第二定律有：2Fcos60°cos37°+f=ma1
N=mg+2Fcos60°sin37°=55N
又因为f=μN
联立方程解得：a1=
| 2F(cos600cos370+μcos600sin370)+μmg |
| m |
代入数据解得：a=7.75m/s2
物体向右运动的最远距离为：s=
0-
| ||
| 2(-a) |
（2）物体向左运动时间t2=t-t1=4s
加速度a=
| 2Fcos600cos370-f |
| m |
6s末时物体的速度v=a2t2=9m/s
力F2的功率P2=F2vcos600cos370=90W
答：（1）在此后物体向右运动的最大距离为15.5m．
（2）6s末时力F2的功率P2为 90W；．
点评：本题主要考查了牛顿第二定律及运动学基本公式的直接应用，要求同学们能正确对物体进行受力分析，难度适中．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
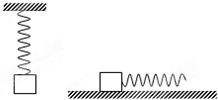原长l0=12cm的弹簧，上端固定，下端挂质量为m=4kg的物块，静止时弹簧长度l1=20cm．当将该物块放在水平桌面上，并用上述弹簧沿水平方向拉物块．当弹簧长度为l2=15cm时，物块恰好被拉动．此后为保持物块做匀速直线运动，弹簧长度维持在l3=14cm．．求：
质量为M=4kg的长木板，上表面粗糙，下表面光滑，静止地放在光滑的水平地面上．在长木板的左、右两端各放着一个小物块A和B，如图所示．已知mA=2kg、mB=1kg，两物块与长木板之间的动摩擦因数都是0.2．现同时用力分别击打A、B，使它们在瞬间同时获得方向相反、大小都是v0=7m/s的水平速度，此后它们在木板上相向滑行，并且在滑行过程中它们始终没有相碰，取g=10m/s2．问：
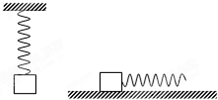原长l0=12cm的弹簧，上端固定，下端挂质量为m=4kg的物块，静止时弹簧长度l1=20cm．当将该物块放在水平桌面上，并用上述弹簧沿水平方向拉物块．当弹簧长度为l2=15cm时，物块恰好被拉动．此后为保持物块做匀速直线运动，弹簧长度维持在l3=14cm．．求：