题目内容
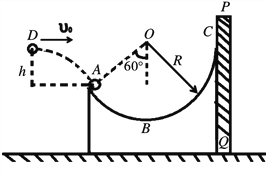
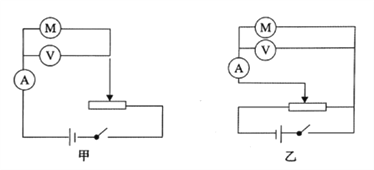
【题目】如图所示,弧形轨道固定于足够长的水平轨道上,弧形轨道与水平轨道平滑连接,水平轨道上静置一小球B和C。小球A从弧形轨道上离地高h处由静止释放,小球A沿轨道下滑后与小球B发生弹性正碰,碰后小球A被弹回,B球与C球碰撞后粘在一起,A球弹回后再从弧形轨道上滚下,已知所有接触面均光滑,A、C两球的质量相等,B球的质量是A球质量的2倍,如果让小球A从h=0.2m处由静止释放,则下列说法正确的是( )(重力加速度为g=10m/s2)

A. A球从h处由静止释放则最后不会与B球再相碰
B. A球从h处由静止释放则最后会与B球再相碰
C. A球从h处由静止释放则C球碰后速度为![]() m/s
m/s
D. A球从h处由静止释放则C球碰后速度为![]() m/s
m/s
【答案】AD
【解析】设A球的质量为m。A从弧形轨道滑到水平轨道的过程中,根据动能定理得: ![]() mv02=mgh,解得:v0=
mv02=mgh,解得:v0=![]()
A与B发生弹性正碰,则碰撞过程中,AB动量守恒,机械能守恒,以A的初速度方向为正方向,由动量守恒和机械能守恒定律得:
mv0=mv1+2mv2,![]() mv02=
mv02=![]() mv12+
mv12+![]() ×2mv22,
×2mv22,
解得:v1=-![]() v0,v2=
v0,v2=![]() v0。
v0。
B与C碰撞过程中,BC组成的系统动量守恒,以B的速度方向为正,根据动量守恒定律得:
2mv2=(2m+m)v
解得:v=![]() v0>|v1|,所以最后A球不会与B球再相碰;故A正确,B错误。当h=0.2m时,根据v0=
v0>|v1|,所以最后A球不会与B球再相碰;故A正确,B错误。当h=0.2m时,根据v0=![]() 、v=
、v=![]() v0可得,C球最后的速度
v0可得,C球最后的速度![]() ,故C错误,D正确。故选AD。
,故C错误,D正确。故选AD。

练习册系列答案
相关题目