题目内容
18.如图甲所示,平行正对金属板A、B间距为d,板长为L,板面水平,加电压后其间匀强电场的场强为E=$\frac{2}{π}$V/m,方向竖直向上.板间有周期性变化的匀强磁场,磁感应强度随时间变化的规律如图乙所示,设垂直纸面向里为正方向.t=0时刻一带电粒子从电场左侧靠近B板处以水平向右的初速度v0开始做匀速直线运动.(设A、B板内侧与粒子绝缘且光滑,重力加速度取g=10m/s2)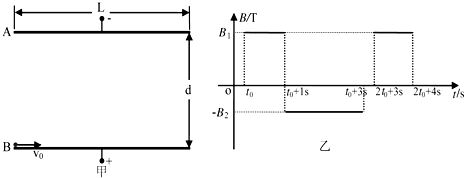
(1)判断粒子电性的正负,并求粒子的比荷
(2)t0时刻起,经过1s粒子第一次速度变为水平向左,则B1多大?
(3)若B2=$\frac{1}{2}$B1,t0=$\frac{2}{π}$s,要使粒子能平行向右到达A板的右端,试求d与L比值的最大值kmax与最小值kmin,并求比值的取值范围△k的最大值.
分析 (1)抓住粒子做匀速直线运动,重力和电场力平衡,根据平衡得出粒子的电性以及比荷的大小.
(2)t0时刻起粒子做匀速圆周运动,经过半个圆周速度第一次变为水平向左,结合周期公式求出磁感应强度的大小.
(3)电场力和重力平衡,粒子在磁场中做圆周运动,根据半径公式求出粒子在不同磁场中做圆周运动的半径,要使粒子能平行向右到达A板右边沿,则粒子在两种磁场中回旋半周的次数相同,结合几何关系进行求解.
解答 解:(1)因为粒子做匀速直线运动,重力与电场力平衡,电场力竖直向上,故粒子带正电.
有:Eq=mg
得:$\frac{q}{m}=\frac{g}{E}=5πC/kg$
(2)t0时刻起粒子做匀速圆周运动,经过半个圆周速度第一次变为水平向左,设粒子在磁感应强度为B1的磁场中运动周期为T1,设粒子质量为m,电荷量为q,
有:${T}_{1}=\frac{2πm}{qB}$,且$\frac{1}{2}$T1=1s
解得:B1=0.2T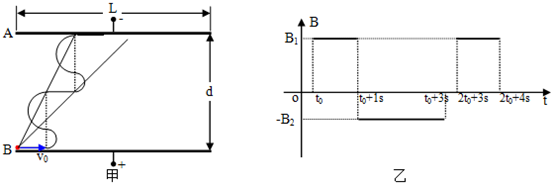
(3)设磁感应强度为B1和B2时粒子运动的半径分别为R1和R2,
有:${R}_{1}=\frac{m{v}_{0}}{q{B}_{1}}=\frac{{v}_{0}}{π}$,${R}_{2}=\frac{m{v}_{0}}{q{B}_{2}}=\frac{2{v}_{0}}{π}$,
要使粒子能平行向右到达A板右边沿,则粒子在两种磁场中回旋半周的次数相同,设为n,有:
$d=2n({R}_{1}+{R}_{2})=\frac{6n{v}_{0}}{π}$,
${L}_{min}=n{v}_{0}{t}_{0}=\frac{2n{v}_{0}}{π}$,Lmax=$(n+1){v}_{0}{t}_{0}=\frac{2(n+1){v}_{0}}{π}$(n=1,2,3,…)
${k}_{max}=\frac{2n({R}_{1}+{R}_{2})}{n{v}_{0}{t}_{0}}=3$,
${k}_{min}=\frac{2n({R}_{1}+{R}_{2})}{(n+1){v}_{0}{t}_{0}}=\frac{3n}{n+1}$,(n=1,2,3,…)
$△k={k}_{max}-{k}_{min}=\frac{3}{n+1}$,当n=1 时,△k有最大值,且最大值为:△kmax=1.5.
答:(1)粒子的比荷为5πC/kg;
(2)B1的大小为0.2T;
(3)比值的取值范围△k的最大值为1.5.
点评 本题考查了带电粒子在复合场中的运动,知道电场力和重力平衡,受洛伦兹力提供向心力,做圆周运动,结合半径公式、周期公式进行求解,第三问对数学能力要求较高,属于压轴部分,需加强这方面的训练.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案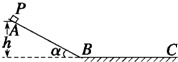 如图所示,可视为质点的滑块P从光滑斜面上的A点由静止开始下滑,经过B点后滑至水平面上,最后停在了C点.对上述过程,在某次实验中,以P刚开始下滑的时刻作为计时的起点(t=0),每隔0.1s通过速度传感器测量物体的瞬时速度,得出的部分测量数据如下表.假设经过B点前后的瞬间,P的速度大小不变,重力加速度g取10m/s2.求:
如图所示,可视为质点的滑块P从光滑斜面上的A点由静止开始下滑,经过B点后滑至水平面上,最后停在了C点.对上述过程,在某次实验中,以P刚开始下滑的时刻作为计时的起点(t=0),每隔0.1s通过速度传感器测量物体的瞬时速度,得出的部分测量数据如下表.假设经过B点前后的瞬间,P的速度大小不变,重力加速度g取10m/s2.求:| t(s) | 0.0 | 0.1 | 0.2 | … | 0.8 | 0.9 | … |
| v(m/s) | 0.0 | 0.5 | 1.0 | … | 2.4 | 2.1 | … |
(2)滑块P与水平面之间的动摩擦因数μ.
(3)A点的高度h.
 形成雾霾天气的主要污染物是PM2.5,为了研究PM2.5的相关性质,某实验小组在实验中让一带电PM2.5颗粒(重力不计),垂直射入正交的匀强电场和磁场区域,如图所示,其中M、N为正对的平行带电金属板,结果它恰能沿直线运动.则( )
形成雾霾天气的主要污染物是PM2.5,为了研究PM2.5的相关性质,某实验小组在实验中让一带电PM2.5颗粒(重力不计),垂直射入正交的匀强电场和磁场区域,如图所示,其中M、N为正对的平行带电金属板,结果它恰能沿直线运动.则( )| A. | M板一定带正电 | |
| B. | PM2.5颗粒一定带正电 | |
| C. | 若仅使PM2.5颗粒的带电量增大,颗粒一定向M板偏移 | |
| D. | 若仅使PM2.5颗粒的速度增大,颗粒一定向N板偏移 |
| A. | 竖直位移旋钮用来调节图象在竖直方向的位置,Y增益旋钮用来调节图象在竖直方向的幅度 | |
| B. | 竖直位移旋钮用来调节图象在竖直方向的幅度,Y增益旋钮用来调节图象在竖直方向的位置 | |
| C. | 竖直位移旋钮和Y增益旋钮都是用来调节图象在竖直方向的位置的 | |
| D. | 竖直位 移旋钮和Y增益旋钮都是用来调节图象在竖直方向的幅度的 |
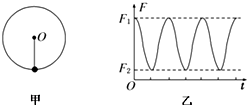 一宇航员到达半径为R、密度均匀的某星球表面,做如下实验,用不可伸长的轻绳栓一质量为m的小球,上端固定在O点,如图甲所示,在最低点给小球某一初速度,使其绕O点在竖直平面内做圆周运动,测得绳的拉力大小随时间t的变化规律如图乙所示,F1=7F2,设R、m、引力常量G、F1、F2均为已知量,忽略各种阻力,以下说法中不正确得是( )
一宇航员到达半径为R、密度均匀的某星球表面,做如下实验,用不可伸长的轻绳栓一质量为m的小球,上端固定在O点,如图甲所示,在最低点给小球某一初速度,使其绕O点在竖直平面内做圆周运动,测得绳的拉力大小随时间t的变化规律如图乙所示,F1=7F2,设R、m、引力常量G、F1、F2均为已知量,忽略各种阻力,以下说法中不正确得是( )| A. | 小球在最高点的最小速度为零 | |
| B. | 卫星绕该星球的第一宇宙速度为$\sqrt{\frac{{R{F_2}}}{m}}$ | |
| C. | 该星球表面的重力加速度为$\frac{F_1}{7m}$ | |
| D. | 星球的质量为$\frac{{{F_2}{R^2}}}{Gm}$ |
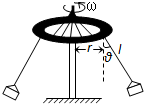 如图所示,这是游乐园的常见的“旋转秋千”项目,游戏开始前,座椅由钢丝绳竖直悬吊在半空.秋千匀速转动时,绳与竖直方向成某一角度θ.现游乐园为安全起见,必须减小秋千转动的线速度,若保持夹角θ不变,可将( )
如图所示,这是游乐园的常见的“旋转秋千”项目,游戏开始前,座椅由钢丝绳竖直悬吊在半空.秋千匀速转动时,绳与竖直方向成某一角度θ.现游乐园为安全起见,必须减小秋千转动的线速度,若保持夹角θ不变,可将( )| A. | 钢丝绳变长 | B. | 钢丝绳变短 | C. | 座椅质量增大 | D. | 座椅质量减小 |
| A. | 向上移动 | B. | 向下移动 | ||
| C. | 不动 | D. | 可能向上移动,也可能向下移动 |
 如图所示两个半径相同的半圆形轨道分别竖直放在匀强电场和匀强磁场中.轨道两端在同一高度上,轨道是光滑的.两个相同的带正电小球同时从两轨道左端最高点由静止释放.M、N为轨道的最低点,下列说法正确的是( )
如图所示两个半径相同的半圆形轨道分别竖直放在匀强电场和匀强磁场中.轨道两端在同一高度上,轨道是光滑的.两个相同的带正电小球同时从两轨道左端最高点由静止释放.M、N为轨道的最低点,下列说法正确的是( )| A. | 两小球到达轨道最低点的速度vM>vN | |
| B. | 两小球第一次到达轨道最低点时对轨道的压力FM>FN | |
| C. | 小球第一次到达M点的时间大于小球第一次到达N点的时间 | |
| D. | 在磁场中小球能到达轨道的另一端,在电场中小球不能到达轨道的另一端 |
