题目内容
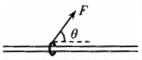
【题目】如图所示,将质量为0.2kg的圆环套在固定的水平直杆上,环的直径略大于杆的直径,环与杆之间的动摩擦因数为0.8.对环施加一位于竖直平面内斜向上的拉力F,使圆环以4.4m/s2的加速度沿杆加速运动,拉力与杆的夹角为![]() ,已知sin
,已知sin![]() =0.8.cos
=0.8.cos![]() =0.6,取g=10m/s2,则F的大小为( )
=0.6,取g=10m/s2,则F的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】BD
【解析】
对环受力分析,受重力、拉力、弹力和摩擦力;令
Fsin53°=mg
解得:
F=2.5N
此时无摩擦力,圆环沿杆做匀加速运动,当F<2.5N 时,杆对环的弹力向上,由牛顿第二定律有:
水平方向上:
Fcosθ-μFN=ma
竖直方向上:
FN+Fsinθ=mg
解得:
F=2N
当F>2.5N时,杆对环的弹力向下,由牛顿第二定律有:
水平方向上有:
Fcosθ-μFN′=ma
竖直方向上有:
Fsinθ=mg+![]()
解得:
F=18N
A.![]() 与分析不符,故A错误;
与分析不符,故A错误;
B.![]() 与分析相符,故B正确;
与分析相符,故B正确;
C.![]() 与分析不符,故C错误;
与分析不符,故C错误;
D.![]() 与分析相符,故D正确。
与分析相符,故D正确。

练习册系列答案
相关题目