题目内容
2.某小型发电站的发电机输出交流电压为500V,输出电功率为50kW,如果用电阻为2Ω的输电线向远处用户送电,这时用户获得的电压和电功率是多少?假如,要求输电线上损失的电功率是输送功率的0.4%,则发电站要安装一个升压变压器,到达用户前再用降压变压器变为220V供用户使用,不考虑变压器的能量损失,这两个变压器原、副线圈的匝数比各是多少?分析 ①根据P损=I2R求出输电线上的电流,分别计算出损失的电压与电功率,即可求出用户获得的电压和电功率.
②根据输电线上的电流和升压变压器的输出功率,求出输出电压,根据原副线圈的电压比等于匝数比求出升压变压器的匝数比.求出输电线上的电压损失,从而得出降压变压器的输入电压,根据降压变压器原副线圈电压比等于匝数比求出降压变压器的匝数比
解答 解:(1)用500V电压输送时,电流:I=$\frac{P}{U}$=$\frac{50×1{0}^{3}}{500}$=100A,
损失的电压:U损=IR=100×2=200V
P损=I2R=1002×2=20KW
所以用户获得的电压U′=500V-300V=200V
电功率为P′=50KW-20KW=30KW.
(2)用高压输送时,示意图如下图所示.要求P损=0.4%P,即P损=50×103×0.4% W=200 W.
输电电流I2=$\sqrt{\frac{{P}_{损}}{R}}$=$\sqrt{\frac{200}{2}}$=10A.
故输电线上的电流为10A.
根据变压器的电流比与匝数比的关系可知:$\frac{{n}_{1}}{{n}_{2}}=\frac{{I}_{2}}{{I}_{1}}$=$\frac{10}{100}$=$\frac{1}{10}$
发电站升压后输电电压U=$\frac{P}{{I}_{2}}$=$\frac{50×1{0}^{3}}{10}$=5×103V
输电线上损失的电压U′=I•R=10×2 V=20 V.
到达用户输入变压器电压
U2=U-U′=(5 000-200)V=4 980 V,
降压变化器的匝数比$\frac{{n}_{3}}{{n}_{4}}$=$\frac{{u}_{2}}{{u}_{3}}$=$\frac{4980}{220}$=$\frac{249}{11}$
答:输出交流电压为500V,用户获得的电压200V,电功率为30KW;
升压变压器和降压变压器的匝数比分别为:1:10,249:11
点评 解决本题的关键知道升压变压器的输出电压、损失电压和降压变压器的输入电压的关系,以及知道输出功率和输出电流和输出电压的关系

 质量相等的A、B两物体置于绕竖直轴匀速转动的水平圆盘上,A与转轴的距离是B与转轴距离的2倍,且始终相对于圆盘静止,则两物体( )
质量相等的A、B两物体置于绕竖直轴匀速转动的水平圆盘上,A与转轴的距离是B与转轴距离的2倍,且始终相对于圆盘静止,则两物体( )| A. | 线速度相同 | B. | 角速度相同 | C. | 向心加速度相同 | D. | 向心力相同 |
 如图所示,轻杆长L=0.4m,一端固定一个小球,另一端绕O轴在竖直面内做圆周运动,当小球到达最高点时瞬间速率为2m/s,重力加速度g=10m/s2,则此时轻杆对小球的作用力的说法正确的是( )
如图所示,轻杆长L=0.4m,一端固定一个小球,另一端绕O轴在竖直面内做圆周运动,当小球到达最高点时瞬间速率为2m/s,重力加速度g=10m/s2,则此时轻杆对小球的作用力的说法正确的是( )| A. | 轻杆对球有拉力 | B. | 轻杆对球有支持力 | ||
| C. | 轻杆对球作用力为零 | D. | 因质量未知无法确定 |
| A. | 伽利略通过斜面实验加逻辑推理的方法研究了自由落体运动的规律 | |
| B. | 开普勒提出了日心说,从而发现了行星运动的规律,后人称为开普勒行星运动规律 | |
| C. | 利用涡流的热效应,人们制成了用于加热食物的电磁炉 | |
| D. | 超高压带电作业的工人穿戴的工作服是用包含金属丝的织物制成的,这是利用了静电屏蔽的原理 |
 如图所示,平行金属板内有一匀强电场,一个电量为q、质量为m的带电粒子(不计重力)以υ0从A点水平射入电场,且刚好以速度υ从B点射出.则下面叙述正确的是( )
如图所示,平行金属板内有一匀强电场,一个电量为q、质量为m的带电粒子(不计重力)以υ0从A点水平射入电场,且刚好以速度υ从B点射出.则下面叙述正确的是( )| A. | 若该粒子以速度-υ从B点射入,则它刚好以速度-υ0从A点射出 | |
| B. | 若将q的反粒子(-q,m)以速度-υ从B点射入,它将刚好以速度-υ0从A点射出 | |
| C. | 若将q的反粒子(-q,m)以速度-υ0从B点射入,它将刚好以速度-υ从A点射出 | |
| D. | 若该粒子以速度-υ0从B点射入电场,它将以速度-υ从A点射出 |
 如图所示,物体在恒力F作用下沿曲线从A运动到B,这时,突然使它受力反向,大小不变,若BD为曲线AB在B点的切线方向,则该物体( )
如图所示,物体在恒力F作用下沿曲线从A运动到B,这时,突然使它受力反向,大小不变,若BD为曲线AB在B点的切线方向,则该物体( )| A. | 可能沿曲线BE运动 | B. | 可能沿曲线BD运动 | ||
| C. | 可能沿曲线BC运动 | D. | 一定是做匀变速直线运动 |
| A. | 曲线运动一定有加速度 | |
| B. | 平抛运动是一种匀变速曲线运动 | |
| C. | 物体受到的合外力是恒力时不会做曲线运动 | |
| D. | 匀速圆周运动是一种变加速曲线运动 |
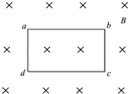 如图所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场垂直.已知线圈的匝数N=100,边长ab=1.0m、bc=0.5m,电阻r=2Ω.磁感应强度B在0-1s内从零均匀变化到0.2T. 在1-5s内从0.2T均匀变化到-0.2T,取垂直纸面向里为磁场的正方向.求:
如图所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场垂直.已知线圈的匝数N=100,边长ab=1.0m、bc=0.5m,电阻r=2Ω.磁感应强度B在0-1s内从零均匀变化到0.2T. 在1-5s内从0.2T均匀变化到-0.2T,取垂直纸面向里为磁场的正方向.求: