题目内容
如右图所示,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动.当它们刚运行至轨道的粗糙段时( )
| A.绳的张力减小,b对a的正压力减小 |
| B.绳的张力增加,斜面对b的支持力增加 |
| C.绳的张力减小,地面对a的支持力增加 |
| D.绳的张力增加,地面对a的支持力减小 |
C
解析试题分析:在光滑段运动时,物块a及物块b均处于平衡状态,对a、b整体受力分析,受重力和支持力,二力平衡
对b受力分析,如上图,受重力、支持力、绳子的拉力,根据共点力平衡条件,有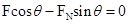 ①;
①;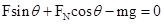 ②;
②;
由①②两式解得: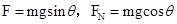 ;
;
当它们刚运行至轨道的粗糙段时,减速滑行,系统有水平向右的加速度,此时有两种可能;
(一)物块a、b仍相对静止,竖直方向加速度为零,由牛顿第二定律得到: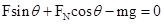 ③;
③;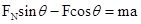 ④;
④;
由③④两式解得: ;
;
即绳的张力F将减小,而a对b的支持力变大;
再对a、b整体受力分析竖直方向重力和支持力平衡,水平方向只受摩擦力,重力和支持力二力平衡,故地面对a支持力不变.
(二)物块b相对于a向上加速滑动,绳的张力显然减小为零,物体具有向上的分加速度,是超重,因此a对b的支持力增大,斜面体和滑块整体具有向上的加速度,也是超重,故地面对a的支持力也增大.
综合上述讨论,结论应该为:绳子拉力一定减小;地面对a的支持力可能增加;a对b的支持力一定增加.故A、B、D错误;
故选C
考点:力的分解与合成,共点力平衡条件
点评:本题关键要熟练运用整体法和隔离法对物体受力,同时要能结合牛顿运动定律求解!解题中还可以运用超重与失重的相关知识

如图,欲使在粗糙斜面上匀速下滑的木块A停下,可采用的方法是 
| A.增大斜面的倾角 |
| B.对木块A施加一个垂直于斜面的力 |
| C.对木块A施加一个竖直向下的力 |
| D.在木块A上再叠放一个重物 |
用一轻绳将小球P系于光滑墙壁上的O点,在墙壁和球P之间夹有一矩形物块Q,如图所示.P、Q均处于静止状态,则下列相关说法正确的是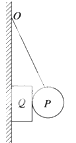
| A.P物体受3个力 |
| B.Q受到3个力 |
| C.若绳子变长,绳子的拉力将变小 |
| D.若绳子变短,Q受到的静摩擦力将增大 |
沿光滑的竖直墙壁用网兜把一个足球挂在A点(如图),足球受到的重力为G,网兜的质量不计。悬绳与墙壁的夹角为α=30o。悬绳给球的拉力为 ,墙壁给球的支持力为
,墙壁给球的支持力为 ,下列表述正确的是( )
,下列表述正确的是( )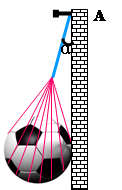
A. 大于G 大于G | B. 小于G 小于G |
C. 与 与 的合力一定竖直向上 的合力一定竖直向上 | D. 与 与 大小之和等于G 大小之和等于G |
如图所示,用绳把球挂在光滑墙壁上的A点,使球静止。如果保持悬挂点A的位置不变,把绳OA的长度加长一些,球仍静止,则绳对球的拉力F1和墙对球的支持力F2的变化情况是( )
| A.F1增大,F2减小 | B.F1减小,F2增大 |
| C.F1和F2都减小 | D.F1和F2都增大 |
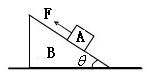
 。斜面上有一质量为m的小物块A,小物块与斜面间存在摩擦。用恒力F沿斜面向上拉小物块,使之匀速上滑。在小物块A运动的过程中,楔形物块B始终保持静止。地面对楔形物块B的支持力为
。斜面上有一质量为m的小物块A,小物块与斜面间存在摩擦。用恒力F沿斜面向上拉小物块,使之匀速上滑。在小物块A运动的过程中,楔形物块B始终保持静止。地面对楔形物块B的支持力为