题目内容
如图所示，半径为R的半圆型光滑绝缘轨道固定在水平面上，一带电量为＋q，质量为m的小球以极微小的速度从轨道最高点A释放，恰在B点进入有界电场和磁场的复合场（电场未画出），并能沿直线运动到地面上的C点。（重力加速度为g）求：
（1）复合场左边界到OA的距离；
（2）电场强度的最小值E，及电场强度最小时匀强磁场的磁感应强度B。
（1）
；（2）
；
解析试题分析：设∠AOB＝θ，小球到B点的速度为v，由动能定理得
mgR（1－cos θ）＝
在B点只受重力，由牛顿第二定律得
mgcos θ＝
联立得
cos θ＝
所以复合场左边界到OA的距离BD＝Rsin θ＝
在磁场和电场的复合场中，受力如图
由共点力平衡得
mgcos θ＝qvB mgsin θ＝qE
联立得
考点： 共点力平衡；带电粒子在复合场中的运动
练习册系列答案
小学课时特训系列答案
相关题目
如右图所示，水平地面上有一楔形物块a，其斜面上有一小物块b，b与平行于斜面的细绳的一端相连，细绳的另一端固定在斜面上．a与b之间光滑，a和b以共同速度在地面轨道的光滑段向左运动．当它们刚运行至轨道的粗糙段时( )
| A．绳的张力减小，b对a的正压力减小 |
| B．绳的张力增加，斜面对b的支持力增加 |
| C．绳的张力减小，地面对a的支持力增加 |
| D．绳的张力增加，地面对a的支持力减小 |
D．
形磁铁的两侧为N极，中心为S极，两级间的磁感应强度大小均为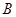
，磁极的宽度均为
，忽略边缘效应.一正方形线圈套于中心磁极，其骨架与秤盘连为一体，线圈两端C、D与外电路连接.当质量为
的重物放在秤盘上时，弹簧被压缩，秤盘和线圈一起向下运动（骨架与磁极不接触），随后外电路对线圈供电，秤盘和线圈恢复到未放重物时的位置并静止，由此时对应的供电电流
可确定重物的质量.已知线圈的匝数为
，线圈的电阻为
，重力加速度为
。问：
，该电子天平能称量的最大质量是多少？
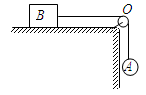
，磁场方向垂直导轨平面向下，磁感应强度的大小为B，平行导轨间距为L。两根金属杆ab和cd可以在导轨上无摩擦地滑动。两金属杆的质量均为m，电阻均为R，导轨的电阻不计。若用与导轨平面平行的拉力F作用在金属杆ab上，使ab匀速上滑，cd杆在导轨上恰好保持静止。求