题目内容
13.有一探测卫星在地球赤道正上方绕地球做匀速圆周运动,已知地球质量为M,万有引力常量为G,探测卫星绕地球运动的周期为T.求:(1)探测卫星绕地球做匀速圆周运动时的轨道半径;
(2)探测卫星绕地球做匀速圆周运动时的速度大小.
分析 (1)卫星绕地球做匀速圆周运动时,由地球的万有引力提供向心力,根据万有引力定律和牛顿第二定律列式求轨道半径.
(2)星绕地球做匀速圆周运动时的速度大小与半径的关系为v=$\frac{2πr}{T}$,与上题结果联立可求得速度大小.
解答 解:(1)设卫星质量为m,卫星绕地球运动的轨道半径为r,根据万有引力定律和牛顿第二定律得:
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
解得:r=$\root{3}{\frac{G{MT}^{2}}{{4π}^{2}}}$
(2)设探测卫星绕地球做匀速圆周运动时的速度大小为v,星绕地球做匀速圆周运动时的速度大小与半径的关系为:
v=$\frac{2πr}{T}$,
即为:v=$\frac{2πr}{T}$=$\root{3}{\frac{2πGM}{T}}$
答:(1)探测卫星绕地球做匀速圆周运动时的轨道半径是$\root{3}{\frac{G{MT}^{2}}{{4π}^{2}}}$;
(2)探测卫星绕地球做匀速圆周运动时的速度大小是$\root{3}{\frac{2πGM}{T}}$.
点评 探测卫星绕地球做匀速圆周运动,关键是万有引力提供向心力列出等式求解.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
4.对下列光学现象的理解正确的是( )
| A. | 两种介质的界面是一个平面,当光线垂直于界面从一种介质进入另一种介质时一定没有反射光线 | |
| B. | 水中的空气泡看上去比较亮是因为气泡对光线有发散作用 | |
| C. | 先后用两种不同的单色光在同一装置同样条件下做双缝干涉实验,在屏上产生的相邻亮纹间距大的单色光,在玻璃中传播速度较大 | |
| D. | 透过卡尺测脚形成的狭缝平行观看日光灯可以看到黑白相间的直条纹 |
5.船要渡过一条流速稳定的小河,关于船渡河的下列说法,正确的是( )
| A. | 船头向着垂直于河岸的方向开行时,航行时间最短 | |
| B. | 船头向着垂直于河岸的方向开行时,实际航程最短 | |
| C. | 实际航线垂直于河岸方向时,航程最短 | |
| D. | 实际航线垂直于河岸方向时,航行时间最短 |
2.下列说法中正确的是( )
| A. | 加速度变化的运动一定是曲线运动 | |
| B. | 物体在恒力和变力作用下,都可能做曲线运动 | |
| C. | 做圆周运动的物体受合外力一定指向圆心 | |
| D. | 物体在恒力作用下不可能做曲线运动 |
3.一个导体球,无论沿着哪个方向的直径测量它的电阻,所得阻值都相等,由此可知,这个导体球( )
| A. | 一定是非晶体 | B. | 可能是单晶体 | C. | 可能是多晶体 | D. | 以上说法都不对 |
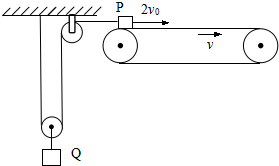 如图所示,一足够长的水平传送带以速度v0匀速运动,质量均为m的小物块P和小物块Q由通过滑轮组的轻绳连接,轻绳足够长且不可伸长.某时刻物块P从传送带左端以速度2v0冲上传送带,P与定滑轮间的绳子水平.已知物块P与传送带间的动摩擦因数μ=0.25,重力加速度为g,不计滑轮的质量与摩擦.求:
如图所示,一足够长的水平传送带以速度v0匀速运动,质量均为m的小物块P和小物块Q由通过滑轮组的轻绳连接,轻绳足够长且不可伸长.某时刻物块P从传送带左端以速度2v0冲上传送带,P与定滑轮间的绳子水平.已知物块P与传送带间的动摩擦因数μ=0.25,重力加速度为g,不计滑轮的质量与摩擦.求: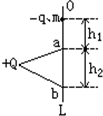 如图所示,L为竖直、固定的光滑绝缘杆,杆上O点套有一质量为m、带电量为-q的小环,在杆的左侧固定一电荷量为+Q的点电荷,杆上a、b两点到+Q的距离相等,Oa之间距离为h1,ab之间距离为h2,使小环从图示位置的O点的由静止释放后,通过a的速率为$\sqrt{3g{h_1}}$.求小环通过b点速率.
如图所示,L为竖直、固定的光滑绝缘杆,杆上O点套有一质量为m、带电量为-q的小环,在杆的左侧固定一电荷量为+Q的点电荷,杆上a、b两点到+Q的距离相等,Oa之间距离为h1,ab之间距离为h2,使小环从图示位置的O点的由静止释放后,通过a的速率为$\sqrt{3g{h_1}}$.求小环通过b点速率.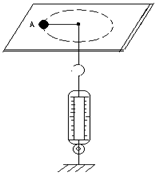 飞船绕地球做匀速圆周运动时处于完全失重状态,在这种环境中已无法用天平称量物体的质量.假设某同学以这种环境设置了如图所示的装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在水平桌面上做匀速圆周运动.设航天器中备有基本测量工具.
飞船绕地球做匀速圆周运动时处于完全失重状态,在这种环境中已无法用天平称量物体的质量.假设某同学以这种环境设置了如图所示的装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在水平桌面上做匀速圆周运动.设航天器中备有基本测量工具.