题目内容
2.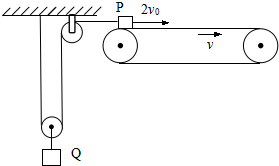 如图所示,一足够长的水平传送带以速度v0匀速运动,质量均为m的小物块P和小物块Q由通过滑轮组的轻绳连接,轻绳足够长且不可伸长.某时刻物块P从传送带左端以速度2v0冲上传送带,P与定滑轮间的绳子水平.已知物块P与传送带间的动摩擦因数μ=0.25,重力加速度为g,不计滑轮的质量与摩擦.求:
如图所示,一足够长的水平传送带以速度v0匀速运动,质量均为m的小物块P和小物块Q由通过滑轮组的轻绳连接,轻绳足够长且不可伸长.某时刻物块P从传送带左端以速度2v0冲上传送带,P与定滑轮间的绳子水平.已知物块P与传送带间的动摩擦因数μ=0.25,重力加速度为g,不计滑轮的质量与摩擦.求:(1)运动过程中小物块P、Q的加速度大小之比;
(2)物块P刚冲上传送带到右方最远处的过程中,PQ系统机械能的改变量;
(3)若传送带以不同的速度v(0<v<2v0)匀速运动,当v取多大时物块P向右冲到最远处时,P与传送带间产生的摩擦热最小?最小值为多大?
分析 (1)由图可知,P与Q的位移关系始终满足P的位移是Q的位移的2倍,结合:$s=\frac{1}{2}a{t}^{2}$求得加速度的比值;
(2)分别以P与Q为研究的对象,由牛顿第二定律求出加速度,然后结合运动学的公式,求出P与传送带的速度相等之前的位移;当P的速度与传送带相等后,分析摩擦力与绳子的拉力的关系,判断出P将继续减速,求出加速度,在结合运动学的公式求出位移,最后由功能关系求出机械能的该变量;
(3)结合(2)的解答过程,写出物体P相对于传送带的位移的表达式以及Q=fx相对,然后即可求出产生的最小的热量.
解答 解:(1)设P的位移、加速度大小分别为s1、a1,Q的位移、加速度大小分别为s2、a2,
因s1=2 s2,故a1=2a2$\frac{{a}_{1}}{{a}_{2}}=\frac{2}{1}$
(2)对P有:μmg+T=ma1
对Q有:mg-2T=ma2
得:T=0.35mg,a1=0.6g
P先减速到与传送带速度相同,设位移为x1,
${x}_{1}=\frac{(2{v}_{0})^{2}-{v}_{0}^{2}}{2{a}_{1}}=\frac{5{v}_{0}^{2}}{2g}$
共速后,由于f=μmg<$\frac{1}{2}$mg,P不可能随传送带一起匀速运动,继续向右减速,
设此时P加速度为a1′,Q的加速度为${a}_{2}′=\frac{1}{2}{a}_{1}′$
对P有:T-μmg=ma1′,对Q有:mg-2T=ma2’解得:a1′=0.2g
设减速到0位移为x2,${x}_{2}=\frac{{v}_{0}^{2}}{2{a}_{1}′}=\frac{5{v}_{0}^{2}}{2g}$
PQ系统机械能的改变量等于摩擦力对P做的功,△E=-μmgx1+μmgx2=0
(3)第一阶段P相对皮带向前,相对路程:${S}_{1}=\frac{(2{v}_{0}-v)^{2}}{2{a}_{1}}$
第二阶段相对皮带向后,相对路程:${S}_{2}=\frac{{v}^{2}}{2{a}_{1}′}$
摩擦产生的热Q=μmg(S1+S2)=$\frac{5}{6}m({v}^{2}-v{v}_{0}+{v}_{0}^{2})$
当$v=\frac{1}{2}{v}_{0}$时,
摩擦热最小$Q=\frac{5}{8}m{v}_{0}^{2}$
答:(1)运动过程中小物块P、Q的加速度大小之比是2:1;
(2)物块P刚冲上传送带到右方最远处的过程中,PQ系统机械能的改变量;
(3)若传送带以不同的速度v(0<v<2v0)匀速运动,当$v=\frac{1}{2}{v}_{0}$时物块P向右冲到最远处时,P与传送带间产生的摩擦热最小,最小值为$\frac{5}{8}m{v}_{0}^{2}$
点评 本题考查牛顿第二定律及功能关系,要注意正确掌握功能的转化关系,明确热量等于摩擦力与相对位移的乘积.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案 如图所示,小车和物体通过轻质细绳相连,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,关于物体的说法正确的是( )
如图所示,小车和物体通过轻质细绳相连,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,关于物体的说法正确的是( )| A. | 物体将匀速上升 | B. | 物体将加速上升 | ||
| C. | 绳的拉力大于A的重力 | D. | 绳的拉力等于A的重力 |
| A. | 光的偏振现象说明光是一种横波 | |
| B. | 雨后路面上的油膜呈现彩色,是光的折射现象 | |
| C. | 相对论认为空间和时间与物质的运动状态无关 | |
| D. | 光导纤维中内层的折射率小于外层的折射率 |
| A. | 卢瑟福通过对α粒子散射实验现象的分析,发现了原子是可以再分的 | |
| B. | β射线与γ射线一样都是电磁波,但穿透本领远比γ射线弱 | |
| C. | 原子核的结合能等于使其完全分解成自由核子所需的最小能量 | |
| D. | 裂变时释放能量是因为发生了亏损质量 |
 如图所示,轻弹簧下端系一重物,O点为其平衡位置(即重力和弹簧弹力大小相等的位置),今用手向下拉重物,第一次把它直接拉到A点,弹力做功为W1,第二次把它拉到B点后再让其回到A点,弹力做功为W2,则这两次弹力做功的关系为( )
如图所示,轻弹簧下端系一重物,O点为其平衡位置(即重力和弹簧弹力大小相等的位置),今用手向下拉重物,第一次把它直接拉到A点,弹力做功为W1,第二次把它拉到B点后再让其回到A点,弹力做功为W2,则这两次弹力做功的关系为( )| A. | W1<W2 | B. | W1=2W2 | C. | W2=2W1 | D. | W1=W2 |

