题目内容
【题目】如图所示，CDE为光滑的轨道，其中ED是水平的，CD是竖直平面内的半圆，与ED相切与D点，且半径R=0．5m，质量m=0．1kg的滑块A静止在水平轨道上，另一质量M=0．5kg的滑块B前端装有一轻质弹簧（A、B均可视为质点）以速度
向左运动并与滑块A发生弹性正碰，若相碰后滑块A滑上半圆轨道并能过最高点C，取重力加速度
，则
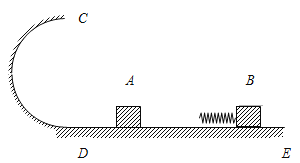
（i）B滑块至少要以多大速度向前运动；
（ii）如果滑块A恰好能过C点，滑块B与滑块A相碰后轻质弹簧的最大弹性势能为多少？
【答案】（i）
（ii）
【解析】
试题分析：（i）设滑块A过C点时速度为
，B与A碰撞后，B与A的速度分别为
，B碰撞前的速度为
过圆轨道最高点的临界条件是重力提供向心力，由牛顿第二定律得
，
由机械能守恒定律得：
，
B与A发生弹性碰撞，碰撞过程动量守恒、机械能守恒，以向右左为正方向，由动量守恒定律得：
，
由机械能守恒定律得：
，
离那里并代入数据解得；
（ii）由于B与A碰撞后，当两者速度相同时有最大弹性势能
，设共同速度为v，A、B碰撞过程系统动量守恒、机械能守恒，以向左为正方向，由动量守恒定律得：
，
由机械能守恒定律得：
，
联立并代入数据解得；
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
