题目内容
16.已知质子的质量是α粒子质量的$\frac{1}{4}$,质子的带电量是α粒子的$\frac{1}{2}$,先让两粒子都由静止开始,经同一加速电场加速,则出电场时,质子的速度与α粒子的速度之比为( )| A. | $\sqrt{2}$:1 | B. | 1:$\sqrt{2}$ | C. | 1:2 | D. | 2:1 |
分析 两个粒子在加速电场中,只有电场力对它们做功,根据动能定理得速度的表达式,再求解速度大小之比.
解答 解:设质子的质量为m,电量为q,加速电场的加速电场为U,根据动能定理得:
qU=$\frac{1}{2}$,得 v=$\sqrt{\frac{2qU}{m}}$
U相同,则知,v与比荷的平方根成正比.α粒子的质量是质子的4倍,电荷量是质子的2倍,则它们比荷之比为$\frac{{q}_{α}}{{m}_{α}}$:$\frac{{q}_{H}}{{m}_{H}}$=1:2
故质子和α粒子获得的速度大小之比为$\sqrt{2}$:1.
故选:A.
点评 带电粒子在加速电场中加速,无论是匀强电场还是非匀强电场,常常运用动能定理求解获得的速度

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
6. (多选)如图所示,甲、乙两电路中是两个完全相同的电源,定值电阻R1>R2.在两电路中分别通过相同电荷量q的过程中,下列判断正确的是( )
(多选)如图所示,甲、乙两电路中是两个完全相同的电源,定值电阻R1>R2.在两电路中分别通过相同电荷量q的过程中,下列判断正确的是( )
 (多选)如图所示,甲、乙两电路中是两个完全相同的电源,定值电阻R1>R2.在两电路中分别通过相同电荷量q的过程中,下列判断正确的是( )
(多选)如图所示,甲、乙两电路中是两个完全相同的电源,定值电阻R1>R2.在两电路中分别通过相同电荷量q的过程中,下列判断正确的是( )| A. | 电源内部产生焦耳热较多的是乙电路 | |
| B. | R1上产生的焦耳热比R2上产生的焦耳热多 | |
| C. | 电源做功较多的是甲电路 | |
| D. | 甲、乙两电路中电源做功相等 |
7. 如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )
如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )
 如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )
如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )| A. | 甲、乙两物体都做匀速运动 | |
| B. | 乙做匀速运动,速度大小为12.5m/s | |
| C. | 甲、乙两物体运动8s后,在距甲的出发点60m处相遇 | |
| D. | 甲在运动过程中停了40s |
4. 平行金属板M、N间为一个正交的匀强电场和匀强磁场区,电场方向由M板指向N极,磁场方向垂直纸面向里,OO′为到两极板距离相等的平行两板的直线.一质量为m,带电量为+q的带电粒子,以v0从O点射入,沿OO′方向匀速通过场区,不计带电粒子的重力,则以下说法正确的是( )
平行金属板M、N间为一个正交的匀强电场和匀强磁场区,电场方向由M板指向N极,磁场方向垂直纸面向里,OO′为到两极板距离相等的平行两板的直线.一质量为m,带电量为+q的带电粒子,以v0从O点射入,沿OO′方向匀速通过场区,不计带电粒子的重力,则以下说法正确的是( )
 平行金属板M、N间为一个正交的匀强电场和匀强磁场区,电场方向由M板指向N极,磁场方向垂直纸面向里,OO′为到两极板距离相等的平行两板的直线.一质量为m,带电量为+q的带电粒子,以v0从O点射入,沿OO′方向匀速通过场区,不计带电粒子的重力,则以下说法正确的是( )
平行金属板M、N间为一个正交的匀强电场和匀强磁场区,电场方向由M板指向N极,磁场方向垂直纸面向里,OO′为到两极板距离相等的平行两板的直线.一质量为m,带电量为+q的带电粒子,以v0从O点射入,沿OO′方向匀速通过场区,不计带电粒子的重力,则以下说法正确的是( )| A. | 带电量为-q的粒子以v0从O点沿OO′方向射入则不能匀速通过场区 | |
| B. | 带电量为2q的粒子以v0从O点沿OO′射入仍能匀速通过场区 | |
| C. | 保持E和B不变,方向均与原来相反,粒子以v0从O点沿OO′射入,则粒子仍能匀速能过场区 | |
| D. | 粒子仍以速率v0从右侧的O′点沿O′O方向射入,粒子仍能匀速能过场区 |
2.用比值定义法定义物理量是一种常用的方法,以下四个物理量都是利用比值定义的,其中不是定义式的是( )
| A. | 电场强度E=$\frac{kQ}{{r}^{2}}$ | B. | 加速度a=$\frac{△v}{△t}$ | C. | 电流强度I=$\frac{q}{t}$ | D. | 电容C=$\frac{?S}{4πkd}$ |
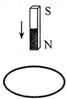 如图所示,桌面上放一100匝线圈,线圈中心上方一定高度处有一竖立的条形磁体.当磁体竖直向下运动时,穿过线圈的磁通量将变大还是变小?.在上述过程中,穿过线圈的磁通量变化了0.1Wb,经历的时间为0.5s,则线圈中的感应电动势为多少伏?
如图所示,桌面上放一100匝线圈,线圈中心上方一定高度处有一竖立的条形磁体.当磁体竖直向下运动时,穿过线圈的磁通量将变大还是变小?.在上述过程中,穿过线圈的磁通量变化了0.1Wb,经历的时间为0.5s,则线圈中的感应电动势为多少伏?
 如图所示,光滑水平地面上,在质量M=1kg的滑块上用轻杆及轻绳悬吊质量m=0.5kg的小球.此装置以速度v0=2m/s向右滑动.另一质量也为M的滑块静止于上述装置的右侧.当两滑块相撞后,便粘在一起向右运动,求
如图所示,光滑水平地面上,在质量M=1kg的滑块上用轻杆及轻绳悬吊质量m=0.5kg的小球.此装置以速度v0=2m/s向右滑动.另一质量也为M的滑块静止于上述装置的右侧.当两滑块相撞后,便粘在一起向右运动,求 如图是一个电压、电流两用表中的两个电流挡,量程为I1=1mA,I2=500mA;一个电压挡,量程为U=10V.已知表头G的满偏电流Ig=500μA,内阻Rg=600Ω,求电阻R1、R2和R3的阻值.(提示:结果为准备值,列出式子得式子分)
如图是一个电压、电流两用表中的两个电流挡,量程为I1=1mA,I2=500mA;一个电压挡,量程为U=10V.已知表头G的满偏电流Ig=500μA,内阻Rg=600Ω,求电阻R1、R2和R3的阻值.(提示:结果为准备值,列出式子得式子分)