题目内容
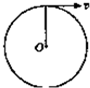
汽车行驶在半径为100m的圆形水平跑道上，速度为20m/s．已知汽车的质量为1000kg，汽车与地面的最大静摩擦力为车重的0.9倍．问：（g=10m/s2）
（1）汽车绕跑道一圈需要的时间是多少？角速度是多少？
（2）汽车在圆形水平跑道上行驶时由什么力提供向心力？向心力是多大？
（3）要使汽车不打滑，则其速度最大不能超过多少？
（1）汽车绕跑道一圈需要的时间是多少？角速度是多少？
（2）汽车在圆形水平跑道上行驶时由什么力提供向心力？向心力是多大？
（3）要使汽车不打滑，则其速度最大不能超过多少？
（1）根据T=
得：T=
=10πs
角速度为：ω=
=
=0.2rad/s
（2）汽车在圆形水平跑道上行驶时由路面对汽车的静摩擦力提供．
由向心力公式有：F向=mRω2
代入数值得：F=1000×100×0.04N=4000（N）
（3）要使汽车不打滑，由路面对汽车的提供的最大向心力等于最大静摩擦力，由牛顿第二定律：
μmg=m
得：v=
=
=30m/s．
答：（1）汽车绕跑道一圈需要的时间是10πs；角速度是0.2rad/s；
（2）汽车在圆形水平跑道上行驶时由静摩擦力提供向心力，向心力大小为4000N．
（3）要使汽车不打滑，则其速度最大不能超过30m/s．
| 2πR |
| V |
| 2π×100 |
| 20 |
角速度为：ω=
| 2π |
| T |
| 2π |
| 10π |
（2）汽车在圆形水平跑道上行驶时由路面对汽车的静摩擦力提供．
由向心力公式有：F向=mRω2
代入数值得：F=1000×100×0.04N=4000（N）
（3）要使汽车不打滑，由路面对汽车的提供的最大向心力等于最大静摩擦力，由牛顿第二定律：
μmg=m
| v2 |
| R |
得：v=
| μgR |
| 0.9×10×100 |
答：（1）汽车绕跑道一圈需要的时间是10πs；角速度是0.2rad/s；
（2）汽车在圆形水平跑道上行驶时由静摩擦力提供向心力，向心力大小为4000N．
（3）要使汽车不打滑，则其速度最大不能超过30m/s．
练习册系列答案
相关题目
