题目内容
 如图示,劲度系数为k的轻质弹簧一端与墙固定,另一端与倾角为θ的斜面体小车连接,小车置于光滑水平面上,在小车上叠放一个物体,已知小车质量为M,物体质量为m,小车位于O点时,整个系统处于平衡状态.现将小车从O点拉到B点,令OB=b,无初速度释放后,小车在水平面B、C间来回运动,物体和小车之间始终没有相对运动.求:
如图示,劲度系数为k的轻质弹簧一端与墙固定,另一端与倾角为θ的斜面体小车连接,小车置于光滑水平面上,在小车上叠放一个物体,已知小车质量为M,物体质量为m,小车位于O点时,整个系统处于平衡状态.现将小车从O点拉到B点,令OB=b,无初速度释放后,小车在水平面B、C间来回运动,物体和小车之间始终没有相对运动.求:(1)小车运动到B点时物体m所受到的摩擦力大小和方向.
(2)b的大小必须满足什么条件,才能使小车和物体在一起运动过程中,在某一位置时,物体和小车之间的摩擦力为零.
分析:(1)小车运动到B点时,先对M和m整体受力分析后根据牛顿第二定律求解出加速度,然后对m,受力分析后根据牛顿第二定律列式求解摩擦力;
(2)在某一位置时,物体和小车之间的摩擦力为零,此时m受重力和支持力,合力向右,故一定是在平衡位置左侧;然后分别对整体和m根据牛顿第二定律列式求解即可.
(2)在某一位置时,物体和小车之间的摩擦力为零,此时m受重力和支持力,合力向右,故一定是在平衡位置左侧;然后分别对整体和m根据牛顿第二定律列式求解即可.
解答:解:(1)取M、m和弹簧组成的系统为研究对象,由牛顿第二定律:kb=(M+m)a (加速度a和摩擦力f是小车在B点时的瞬时值);
所以a=
;
取m为研究对象,受重力、支持力和摩擦力(沿斜面向上 ),在沿斜面方向有:f-mgsinθ=macosθ;
解得f=mgsinθ+
;
(2)当物体和小车之间的摩擦力的零时,小车的加速度变为a',小车距O点距离为 b',
取m为研究对象,有:mgsinθ=ma'cosθ
取M、m和弹簧组成的系统为研究对象,有:kb'=(M+m)a'
以上述两式联立解得:b'=
;
由于简谐运动具有对称性,故b=b′=
;
答:(1)小车运动到B点时物体m所受到的摩擦力大小为mgsinθ+
,方向为沿斜面向上;
(2)b的大小大于或等于
时,才能使小车和物体在一起运动过程中,在某一位置时,物体和小车之间的摩擦力为零.
所以a=
| kb |
| M+m |
取m为研究对象,受重力、支持力和摩擦力(沿斜面向上 ),在沿斜面方向有:f-mgsinθ=macosθ;
解得f=mgsinθ+
| kbmcosθ |
| M+m |
(2)当物体和小车之间的摩擦力的零时,小车的加速度变为a',小车距O点距离为 b',
取m为研究对象,有:mgsinθ=ma'cosθ
取M、m和弹簧组成的系统为研究对象,有:kb'=(M+m)a'
以上述两式联立解得:b'=
| (M+m)gtanθ |
| k |
由于简谐运动具有对称性,故b=b′=
| (M+m)gtanθ |
| k |
答:(1)小车运动到B点时物体m所受到的摩擦力大小为mgsinθ+
| kbmcosθ |
| M+m |
(2)b的大小大于或等于
| (M+m)gtanθ |
| k |
点评:本题关键先根据整体法求解加速度,然后再隔离m受力分析并根据牛顿第二定律列式求解,不难.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
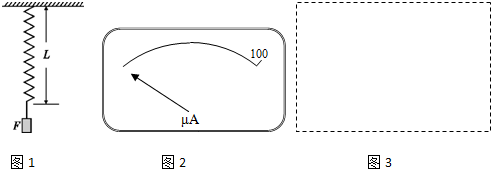
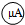 的刻度盘只标注了表示量程Ig=100μA的刻度线,尚未标注其他分刻度线,如图所2示.请用下列全部器材测量微安表
的刻度盘只标注了表示量程Ig=100μA的刻度线,尚未标注其他分刻度线,如图所2示.请用下列全部器材测量微安表 的内阻:
的内阻: :内阻Rg约为2kΩ
:内阻Rg约为2kΩ :量程250mV,最小分度5mV,内阻约为1kΩ
:量程250mV,最小分度5mV,内阻约为1kΩ 的内阻Rg的实验电路原理图(原理图中的元①要用相应的英文字母标注).
的内阻Rg的实验电路原理图(原理图中的元①要用相应的英文字母标注). 的内阻Rg=
的内阻Rg= 如图所示,在水平传送带上有三个质量分别为 m、2m、3m的木块1、2、3,中间分别用一原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数为μ,现用水平细绳将木块1固定在左边的墙上,传送带按图示方向匀速运动,当三个木块达到平衡后,1、2两木块之间的距离是( )
如图所示,在水平传送带上有三个质量分别为 m、2m、3m的木块1、2、3,中间分别用一原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数为μ,现用水平细绳将木块1固定在左边的墙上,传送带按图示方向匀速运动,当三个木块达到平衡后,1、2两木块之间的距离是( ) 如图所示,在倾角为α的传送带上有质量均为m的三个木块1、2、3,中间均用原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细绳拉住,传送带按图示方向匀速运动,三个木块处于平衡状态.下列结论正确的是( )
如图所示,在倾角为α的传送带上有质量均为m的三个木块1、2、3,中间均用原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细绳拉住,传送带按图示方向匀速运动,三个木块处于平衡状态.下列结论正确的是( ) 如图示,劲度系数为k的轻质弹簧一端与墙固定,另一端与倾角为θ的斜面体小车连接,小车置于光滑水平面上,在小车上叠放一个物体,已知小车质量为M,物体质量为m,小车位于O点时,整个系统处于平衡状态.现将小车从O点拉到B点,令OB=b,无初速度释放后,小车在水平面B、C间来回运动,物体和小车之间始终没有相对运动.求:
如图示,劲度系数为k的轻质弹簧一端与墙固定,另一端与倾角为θ的斜面体小车连接,小车置于光滑水平面上,在小车上叠放一个物体,已知小车质量为M,物体质量为m,小车位于O点时,整个系统处于平衡状态.现将小车从O点拉到B点,令OB=b,无初速度释放后,小车在水平面B、C间来回运动,物体和小车之间始终没有相对运动.求: