题目内容
3. 如图所示,在xOy坐标平面内的第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q点,圆内存在垂直xOy平面的匀强磁场.在第Ⅰ象限内存在沿y轴方向的匀强电场,电场强度为E.一质量为m、电荷量为q的粒子从P点射入磁场后恰好垂直y轴进入电场,最后从M(2R,0)点射出电场,出射方向与x轴夹角α满足tanα=1.5.求:
如图所示,在xOy坐标平面内的第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q点,圆内存在垂直xOy平面的匀强磁场.在第Ⅰ象限内存在沿y轴方向的匀强电场,电场强度为E.一质量为m、电荷量为q的粒子从P点射入磁场后恰好垂直y轴进入电场,最后从M(2R,0)点射出电场,出射方向与x轴夹角α满足tanα=1.5.求:(1)粒子进入电场时的速率v0;
(2)匀强磁场的磁感应强度B;
(3)粒子从P点入射的方向与x轴负方向的夹角θ.
分析 (1)粒子垂直于电场进入第一象限,粒子做类平抛运动,由到达M的速度方向可利用速度的合成与分解得知该点y方向的速度.结合牛顿第二定律求得粒子的速率v0;
(2)根据运动学的公式,求出粒子进入电场时的位置,画出粒子运动的轨迹,根据图象中的几何关系求出粒子运动的半径,根据半径公式r=$\frac{mv}{qB}$求出磁感应强度B;
(3)粒子在洛伦兹力的作用下做匀速圆周运动,利用洛伦兹力提供向心力的公式,求出在磁场中运动的轨迹半径,利用几何关系求θ.
解答 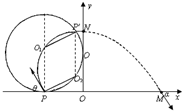 解:(1)在M处,粒子的y轴分速度
解:(1)在M处,粒子的y轴分速度
vy=2v0tanα
设粒子在电场中运动时间为t,在x轴方向匀速运动:
2R=v0t
设y轴方向匀加速运动的加速度为a,由
qE=ma;
且vy=at
联立解得:v0=$\sqrt{\frac{4RqE}{3m}}$
(2)如图所示,O1为磁场圆的圆心,O2为粒子轨迹圆的圆心,P′为粒子射出磁场的位置,依题意可知粒子垂直y轴进入电场,则P′O2∥PO1,且P′O1∥PO1=R,O2P=O2P′,由几何关系可知O1P′O2P为菱形,即粒子轨迹圆半径等于R.
由向心力公式及牛顿第二定律:$Bq{v_0}=m\frac{v_0^2}{R}$;
联立解得:B=$\sqrt{\frac{4Em}{3qR}}$
(3)粒子从N点进入电场,由y轴方向匀加速直线运动公式有NO的长度y满足
vy2=2ay
联立解得:y=1.5R;
由几何关系:R+Rcosθ=y.解得:θ=60°
答:
(1)粒子进入电场时的速率v0为$\sqrt{\frac{4RqE}{3m}}$.
(2)匀强磁场的磁感应强度B为$\sqrt{\frac{4Em}{3qR}}$;
(3)粒子从P点入射的方向与x轴负方向的夹角θ是60°.
点评 粒子在电场中运动偏转时,常用能量的观点来解决问题,有时也要运用运动的合成与分解.粒子在磁场中做匀速圆周运动的圆心、半径及运动时间的确定也是本题的一个考查重点,要正确画出粒子运动的轨迹图,能熟练运用几何知识解决物理问题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案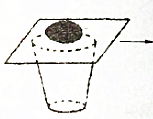 如图所示,一只杯子固定在水平桌面上,将一块薄纸板盖在杯口并在纸板上放一枚鸡蛋,现用水平向右的拉力将纸板快速抽出,鸡蛋(水平移动距离很小,几乎看不到)掉入杯中,这就是惯性演示.已知鸡蛋(可视为质点)中心离纸板左端的距离为d,鸡蛋和纸板的质量分别为m和2m,所有接触面的动摩擦因数均为μ,重力加速度为g,若鸡蛋移动的距离不超过$\frac{d}{10}$就能保证实验成功,则所需拉力的最小值为( )
如图所示,一只杯子固定在水平桌面上,将一块薄纸板盖在杯口并在纸板上放一枚鸡蛋,现用水平向右的拉力将纸板快速抽出,鸡蛋(水平移动距离很小,几乎看不到)掉入杯中,这就是惯性演示.已知鸡蛋(可视为质点)中心离纸板左端的距离为d,鸡蛋和纸板的质量分别为m和2m,所有接触面的动摩擦因数均为μ,重力加速度为g,若鸡蛋移动的距离不超过$\frac{d}{10}$就能保证实验成功,则所需拉力的最小值为( )| A. | 3μmg | B. | 26μmg | C. | 12μmg | D. | 15μmg |
| A. | 加速度和线速度保持不变 | B. | 周期和角速度保持不变 | ||
| C. | 合外力始终指向圆心 | D. | 合外力保持不变 |
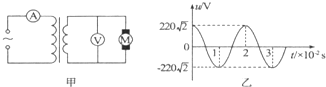
| A. | 通过小电动机电流的频率为50Hz | |
| B. | 原线圈输入的交变电压的瞬时值表达式为u=220cos50πt(V) | |
| C. | 电流表的示数为0.05A | |
| D. | 如果电动机转子突然被卡住不转,变压器的输入功率减小 |
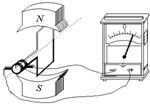
| A. | 指针随着线圈转动而摆动,并且线圈旋转一周,指针左右摆动一次 | |
| B. | 当线圈平面转到跟磁力线垂直的平面位置时,电流表的指针的偏转最大 | |
| C. | 当线圈平面转到跟磁力线平行的位置时,电流表的指针的偏转最大 | |
| D. | 在匀强磁场中匀速转动的线圈里产生感应电动势和感应电流是按正弦规律变化的 |
| A. | 牛顿是动力学的奠基人,他总结和发展了前人的成果,发现了力和运动的关系 | |
| B. | 法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机──法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕 | |
| C. | 重心、合力和交变电流的有效值等概念的建立都体现了等效替代的思想 | |
| D. | 变压器的铁芯使用了硅钢片,这样在铁芯中就不会产生任何涡流 |
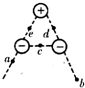 在真空中三个等量点电荷固定在正三角形的三个顶点,如图所示,c、d、e为三角形三个边的中点,下列判断正确的是( )
在真空中三个等量点电荷固定在正三角形的三个顶点,如图所示,c、d、e为三角形三个边的中点,下列判断正确的是( )| A. | d、e两点的电场强度相同 | |
| B. | d、e两点的电势相等 | |
| C. | 电子在a点的电势能高于在b点的电势能 | |
| D. | d点的场强大于c点的场强 |
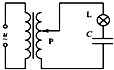 如图所示,理想变压器原线圈接有交流电源,当副线圈上的滑片P处于图示位置时,灯泡L能发光. 要使灯泡变亮,可以采取的方法有( )
如图所示,理想变压器原线圈接有交流电源,当副线圈上的滑片P处于图示位置时,灯泡L能发光. 要使灯泡变亮,可以采取的方法有( )| A. | 向下滑动P | B. | 减小电容器C的电容 | ||
| C. | 减小交流电源的频率 | D. | 增大交流电源的电压 |
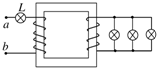 如图所示,在一理想变压器的初、次级线圈接有4个相同的灯泡,若4个灯泡都正常发光,则该变压器初、次级线圈的匝数比n1:n2等于( )
如图所示,在一理想变压器的初、次级线圈接有4个相同的灯泡,若4个灯泡都正常发光,则该变压器初、次级线圈的匝数比n1:n2等于( )