题目内容
4.甲车以10m/s的速度在平直的公路上匀速行驶,乙车以4m/s的速度与甲车平行同向做匀速直线运动.甲车经过乙车旁边时开始以0.5m/s2的加速度刹车,从甲车刹车开始计时,求:(1)乙车在追上甲车前,两车相距的最大距离;
(2)乙车追上甲车所用的时间.
分析 (1)当两车速度相等时,两车间的距离最大.根据速度相等条件求出时间,分别求出两车的位移,两者之差等于它们间的距离.
(2)由题,甲车甲车做匀减速直线运动,乙车做匀速直线运动,当两车的位移相同时,乙车追上甲车.根据位移公式列方程求解时间.
解答 解:(1)在乙车追上甲车之前,当两车速度相等时两车间的距离最大,设此时经过的时间为t,则有:
v2=v1-at
代入数据得:t=12s
此时甲车的位移为:x1=v1t-$\frac{1}{2}$at2=10×12-$\frac{1}{2}×0.5×1{2}^{2}$m=84m
乙车的位移为:x2=v2t=4×12m=48m
所以两车间的最大距离为:
△x=x2-x1=84-48m=36m
(2)设甲车停止的时间为t1,则有:${t}_{1}=\frac{{v}_{1}}{a}=\frac{10}{0.5}s=20s$,
甲车在这段时间内发生的位移为:$x=\frac{{v}_{1}^{2}}{2a}=\frac{1{0}^{2}}{2×0.5}m=100m$
乙车发生的位移为:
x′=v′t1=4×20m=80m
可知,甲车停止时,乙车还没有追上甲车,则 乙车追上甲车所用的时间为:
t2=t1+$\frac{100-80}{4}$=20+5s=25s
答:(1)乙车追上甲车前,两车相距的最大距离36m;
(2)乙车追上甲车所用的时间25s.
点评 本题是追及问题,在分别研究两车运动的基础上,关键是研究两者之间的关系,通常有位移关系、速度关系、时间关系

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
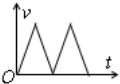
14.某物体作直线运动的v-t图线如图所示,则该物体( )

| A. | 做往复运动 | B. | 做匀变速直线运动 | ||
| C. | 朝某一方向做直线运动 | D. | 以上说法均不正确 |
15.关于路程和位移,下列说法正确的是( )
| A. | 沿直线运动的物体,位移和路程是相等的 | |
| B. | 质点通过一段路程,其位移可能为零 | |
| C. | 质点运动的位移大小可能大于路程 | |
| D. | 质点沿不同的路径由A到B,其路程可能不同而位移是相同的 |
12.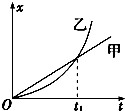 甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻作为计时起点得到两车的位移--时间图象如图所示,则下列说法正确的是( )
甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻作为计时起点得到两车的位移--时间图象如图所示,则下列说法正确的是( )
 甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻作为计时起点得到两车的位移--时间图象如图所示,则下列说法正确的是( )
甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻作为计时起点得到两车的位移--时间图象如图所示,则下列说法正确的是( )| A. | t1时刻甲车从后面追上乙车 | B. | t1时刻两车相距最远 | ||
| C. | t1时刻两车的速度刚好相等 | D. | 0到t1时间内,两车的平均速度相等 |
19.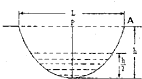 如图所示,有一个截面为抛物面形状的水池(所画平面图为抛物线),水池最深处为h=5m,池子口跨度为L=10m.其中水的最大深度为$\frac{h}{2}$.有一根竖直杆插在水池中心处,杆的项端恰与池子口在同一水平面上,杆的顶端有一只青娃,它沿图示PA方向水平跳出.为了能落入水中,它的跳出速度最大是(g=10m/s2)( )
如图所示,有一个截面为抛物面形状的水池(所画平面图为抛物线),水池最深处为h=5m,池子口跨度为L=10m.其中水的最大深度为$\frac{h}{2}$.有一根竖直杆插在水池中心处,杆的项端恰与池子口在同一水平面上,杆的顶端有一只青娃,它沿图示PA方向水平跳出.为了能落入水中,它的跳出速度最大是(g=10m/s2)( )
 如图所示,有一个截面为抛物面形状的水池(所画平面图为抛物线),水池最深处为h=5m,池子口跨度为L=10m.其中水的最大深度为$\frac{h}{2}$.有一根竖直杆插在水池中心处,杆的项端恰与池子口在同一水平面上,杆的顶端有一只青娃,它沿图示PA方向水平跳出.为了能落入水中,它的跳出速度最大是(g=10m/s2)( )
如图所示,有一个截面为抛物面形状的水池(所画平面图为抛物线),水池最深处为h=5m,池子口跨度为L=10m.其中水的最大深度为$\frac{h}{2}$.有一根竖直杆插在水池中心处,杆的项端恰与池子口在同一水平面上,杆的顶端有一只青娃,它沿图示PA方向水平跳出.为了能落入水中,它的跳出速度最大是(g=10m/s2)( )| A. | 3m/s | B. | 4m/s | C. | 5m/s | D. | 6m/s |
16.下列说法正确的是( )
| A. | 做平抛运动的物体加速度一直增大 | |
| B. | 做圆周运动的物体,其加速度一定指向圆心 | |
| C. | 不共线的两个初速度不为零的匀变速直线运动的合运动一定是匀变速运动 | |
| D. | 物体在恒力作用下做曲线运动,在相同时间内的速度变化量一定相同 |
2.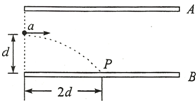 如图,水平放置的平行板电容器极板A、B间加有恒定电压,a点与下极板的距离为d.一带电粒子从a点水平射入电场,初速度大小为va,粒子偏转后打在下极板的P点时速度大小为va′,其水平射程为2d.若该粒子从与a在同一竖直线上的b点(图中未标出)水平射入电场,初速度大小为vb,带电粒子仍能打到P点,打到P点时速度大小为vb′.下列判断正确的是( )
如图,水平放置的平行板电容器极板A、B间加有恒定电压,a点与下极板的距离为d.一带电粒子从a点水平射入电场,初速度大小为va,粒子偏转后打在下极板的P点时速度大小为va′,其水平射程为2d.若该粒子从与a在同一竖直线上的b点(图中未标出)水平射入电场,初速度大小为vb,带电粒子仍能打到P点,打到P点时速度大小为vb′.下列判断正确的是( )
 如图,水平放置的平行板电容器极板A、B间加有恒定电压,a点与下极板的距离为d.一带电粒子从a点水平射入电场,初速度大小为va,粒子偏转后打在下极板的P点时速度大小为va′,其水平射程为2d.若该粒子从与a在同一竖直线上的b点(图中未标出)水平射入电场,初速度大小为vb,带电粒子仍能打到P点,打到P点时速度大小为vb′.下列判断正确的是( )
如图,水平放置的平行板电容器极板A、B间加有恒定电压,a点与下极板的距离为d.一带电粒子从a点水平射入电场,初速度大小为va,粒子偏转后打在下极板的P点时速度大小为va′,其水平射程为2d.若该粒子从与a在同一竖直线上的b点(图中未标出)水平射入电场,初速度大小为vb,带电粒子仍能打到P点,打到P点时速度大小为vb′.下列判断正确的是( )| A. | 若b点在a点上方,则va<vb | B. | 若b点在a点下方,则va>vb | ||
| C. | 若b点在a点上方,则va′<vb′ | D. | 若b点在a点下方,则va′>vb′ |