题目内容
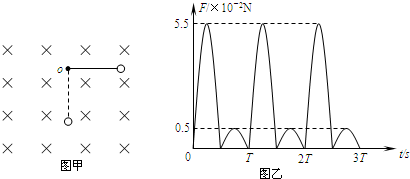
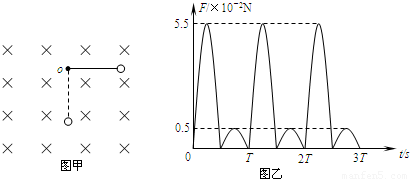
如图甲，用一根长L=0.8m的绝缘不可伸长的轻质细绳，将一带电小球悬挂在O点，整个装置处在垂直纸面向里的匀强磁场中．现将小球从悬点O的右侧水平位置由静止释放（绳刚好拉直），小球便在垂直磁场的竖直平面内左右摆动．用拉力传感器（图中未画出）测出绳中的拉力F随时间t变化规律如图乙（取重力加速度g=10m/s2）．求：
（1）小球带何种电荷；
（2）小球运动到最低点时速度大小；
（3）小球的质量．
（1）小球带何种电荷；
（2）小球运动到最低点时速度大小；
（3）小球的质量．
分析：（1）结合两图可以看出，小球从左往右运动时的拉力大于小球从右向左运动时的拉力，在最低点受力分析，可知小球的电性．
（2）根据动能定理，洛伦兹力不做功，只有重力做功，求出最低点的速度．
（3）在最低点受力分析，在竖直方向上的合力提供向心力，小球向左通过最低点时，有F1-mg-qvB=m
，小球向右通过最低点时，有F2-mg+qvB=m
．联立两方程组求出质量．
（2）根据动能定理，洛伦兹力不做功，只有重力做功，求出最低点的速度．
（3）在最低点受力分析，在竖直方向上的合力提供向心力，小球向左通过最低点时，有F1-mg-qvB=m
| v2 |
| L |
| v2 |
| L |
解答：解：（1）小球从左往右运动时的拉力大于小球从右向左运动时的拉力，知从左往右运动时洛伦兹力向下，根据左手定则，知小球带正电荷．
（2）由动能定理 mgL=
mv2 解得 v=
=4m/s
（3）根据牛顿定律，小球向左通过最低点时 F1-mg-qvB=m
小球向右通过最低点时 F2-mg+qvB=m
由以上各式解得 m=1g
（2）由动能定理 mgL=
| 1 |
| 2 |
| 2gL |
（3）根据牛顿定律，小球向左通过最低点时 F1-mg-qvB=m
| v2 |
| L |
小球向右通过最低点时 F2-mg+qvB=m
| v2 |
| L |
由以上各式解得 m=1g
点评：解决本题的关键掌握洛伦兹力的方向，以及熟练掌握动能定理，知道在最低点在竖直方向上的合力提供向心力．
练习册系列答案
相关题目
如图所示，一根长为L、质量为100kg的木头，其重心O在离粗端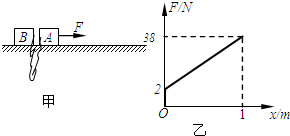
如图甲所示两滑块A、B并排静止在水平面上，它们中间用一根长L=1m的轻绳（松驰）相连，在滑块A上有一个从零逐渐增大的拉力作用一段距离后撤除，其大小F与滑块A的位移x关系如图乙所示，已知mA=1kg、mB=2kg，轻绳从张紧到崩直时间极短并没有崩断，两滑块与水平面间的动摩擦因数相同且最大静摩擦力等于滑动摩擦力．g取10m/s2，试求：
