题目内容
【题目】如图甲所示的坐标系中,第四限象内存在垂直于纸面向里的有界匀强磁场,x方向的宽度OA=20![]() cm,y方向无限制,磁感应强度B0=1×10-4T。现有一比荷为
cm,y方向无限制,磁感应强度B0=1×10-4T。现有一比荷为![]() =2×1011C/kg的正离子以某一速度从O点射入磁场,α=60°,离子通过磁场后刚好从A点射出。
=2×1011C/kg的正离子以某一速度从O点射入磁场,α=60°,离子通过磁场后刚好从A点射出。

(1)求离子进入磁场B0的速度的大小;
(2)离子进入磁场B0后,某时刻再加一个同方向的匀强磁场,使离子做完整的圆周运动,求所加磁场磁感应强度的最小值;
(3)离子进入磁场B0后,再加一个如图乙所示的变化磁场(正方向与B0方向相同,不考虑磁场变化所产生的电场),求离子从O点到A点的总时间。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
离子在磁场中做匀速圆周运动,轨道半径可由几何关系求得,洛仑兹力提供向心力,根据向心力公式即可求得速度;根据牛顿第二定律和几何关系求得半径,再根据向心力公式即可求得B,进而求出外加磁场最小值;先算出离子在磁场中运动第一次遇到外加磁场的过程中轨迹对应的圆心角,由几何关系求出此时施加附加磁场时离子在磁场中能做的圆周运动的最大半径,根据向心力公式求出离子在有附加磁场时运动半径,判断粒子是否能做完整的圆周运动,对照外加磁场的规律求出粒子做圆周运动的次数,最后求得总时间。
(1)粒子轨迹如图所示:
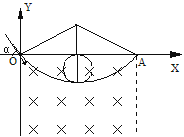
由几何关系得离子在磁场中运动时的轨道半径![]()
离子在磁场中做匀速圆周运动,洛仑兹力提供向心力:![]()
求得:![]()
(2)由![]() 知,B越小,r越大。设离子在磁场中最大半径为R
知,B越小,r越大。设离子在磁场中最大半径为R
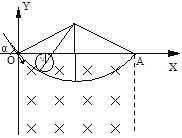
由几何关系得:![]()
由牛顿运动定律得![]()
求得![]()
则外加磁场![]()
(3)离子在原磁场中运动周期:![]()
离子在磁场中运动第一次遇到外加磁场的过程中轨迹对应的圆心角
![]()
此时施加附加磁场时离子在磁场中能做的圆周运动的最大半径为r2
由几何关系知:![]()
离子在有附加磁场时运动半径为r3,则![]()
求得![]()
因![]() ,所以离子能做完整的圆周运动
,所以离子能做完整的圆周运动
离子在外加磁场后时, ![]()
对照外加磁场的规律可知,每隔![]() 离子在周期性外加磁场时,离子恰可做一次完整的匀速圆周运动,共做三次,最后在A点离开磁场。
离子在周期性外加磁场时,离子恰可做一次完整的匀速圆周运动,共做三次,最后在A点离开磁场。
离子从O点进入到A点射出的总时间为![]()

【题目】一实验小组准备探究某种元件Q的伏安特性曲线,他们设计了如图所示的电路图。请回答下列问题:



(1)请将图中的实物连线按电路图补充完整 _______。
(2)考虑电表内阻的影响,该元件电阻的测量值__________(选填“大于”、“等于”或“小于”)真实值。
(3)在电路图中闭合开关S,电流表、电压表均有示数,但无论怎样移动变阻器滑动片,总不能使电压表的示数调为零。原因可能是图中的______(选填a、b、c、d、e、f)处接触不良。
(4)实验测得表格中的7组数据。请在坐标纸上作出该元件的I-U图线___________。
(5)为了求元件Q在I-U图线上某点的电阻,甲同学利用该点的坐标I、U,由![]() 求得。乙同学作出该点的切线,求出切线的斜率k,由
求得。乙同学作出该点的切线,求出切线的斜率k,由![]() 求得。其中______(选填“甲”、“乙”)同学的方法正确。
求得。其中______(选填“甲”、“乙”)同学的方法正确。
序号 | 电压/V | 电流/A |
1 | 0.00 | 0.00 |
2 | 0.40 | 0.02 |
3 | 0.80 | 0.05 |
4 | 1.20 | 0.12 |
5 | 1.60 | 0.20 |
6 | 2.00 | 0.31 |
7 | 2.40 | 0.44 |