题目内容
【题目】如图所示,有一矩形区域abcd,水平方向ab边长L1= ![]() m,竖直方向ad边长L2=1m,一电荷量为q=1×10﹣5C,质量为m=6×10﹣6kg的带正电的粒子由a点沿ab方向以大小为2m/s的速度v进入该区域.当该区域存在与纸面垂直的匀强磁场时,粒子的运动轨迹恰好通过该区域的几何中心O点,不计粒子的重力,求:
m,竖直方向ad边长L2=1m,一电荷量为q=1×10﹣5C,质量为m=6×10﹣6kg的带正电的粒子由a点沿ab方向以大小为2m/s的速度v进入该区域.当该区域存在与纸面垂直的匀强磁场时,粒子的运动轨迹恰好通过该区域的几何中心O点,不计粒子的重力,求: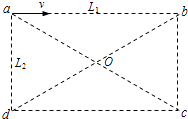
(1)粒子在磁场区域运动的半径大小;
(2)匀强磁场的磁感应强度大小和方向;
(3)粒子通过磁场区域所用的时间.
【答案】
(1)解:作出粒子在磁场中偏转运动的轨迹如图所示;
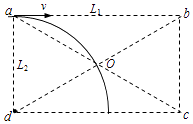
由题意可知aO长度L=1m,由圆的规律可知,d点就是轨迹的圆心
由几何关系可知,轨迹半径为:R=L2=1m
答:粒子在磁场区域运动的半径大小为1m;
(2)解:根据左手定则,可以判断磁场的方向垂直于纸面向外
由qvB=m ![]()
解得 B= ![]() =
= ![]() =1.2T
=1.2T
答:匀强磁场的磁感应强度大小和方向为1.2T,方向垂直纸面向外;
(3)解:由题意可知和对应的图象可知,磁场中的运动轨迹为 ![]() 圆弧,所以由
圆弧,所以由
t= ![]() 可得:
可得:
t= ![]() =
= ![]() =
= ![]() =0.785s.
=0.785s.
答:粒子通过磁场区域所用的时间为0.785s.
【解析】(1)由题意明确粒子的运动轨迹,由几何关系即可明确粒子的转动半径;(2)根据左手定则可明确磁场的方向;再根据洛伦兹力充当向心力列式即可求得磁感应强度的大小;(3)明确粒子在磁场中转过的圆心角和弦长,再根据线速度公式即可求得运动时间.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目