题目内容
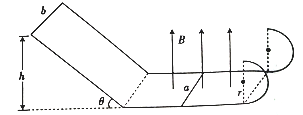
【题目】如图所示,宽度为L=0.2m的水平平行光滑的金属轨道,左端连接动摩擦因数为![]() 、倾角为θ=30°的斜面轨道(斜面轨道下端与水平光滑轨道之间有一小圆弧平滑连接),右端连接半径为r=0.15m的光滑半圆轨道,水平轨道与半圆轨道相切。水平轨道所在的区域处在磁感应强度大小为B=1T的竖直向上的匀强磁场中。一根质量为m=0.1kg的金属杆a 置于水平轨道上,另一根质量为M=0.5kg的金属杆b从斜面轨道上与水平轨道高度为h=0.4m处由静止释放,当金属杆b滑入水平轨道某位置时,金属杆a刚好到达半圆轨道最高点(b始终运动且a、b未相撞),并且a在半圆轨道最高点对轨道的压力大小等于金属杆a的重力, 此过程中通过金属杆a的电荷量为q=4C, a、b杆的电阻分别为R1=0.1Ω、R2=0.3Ω,其余部分电阻不计。(g取10m/s2)求:
、倾角为θ=30°的斜面轨道(斜面轨道下端与水平光滑轨道之间有一小圆弧平滑连接),右端连接半径为r=0.15m的光滑半圆轨道,水平轨道与半圆轨道相切。水平轨道所在的区域处在磁感应强度大小为B=1T的竖直向上的匀强磁场中。一根质量为m=0.1kg的金属杆a 置于水平轨道上,另一根质量为M=0.5kg的金属杆b从斜面轨道上与水平轨道高度为h=0.4m处由静止释放,当金属杆b滑入水平轨道某位置时,金属杆a刚好到达半圆轨道最高点(b始终运动且a、b未相撞),并且a在半圆轨道最高点对轨道的压力大小等于金属杆a的重力, 此过程中通过金属杆a的电荷量为q=4C, a、b杆的电阻分别为R1=0.1Ω、R2=0.3Ω,其余部分电阻不计。(g取10m/s2)求:
(1)金属杆b在水平轨道上运动时的最大加速度![]() ;
;
(2)在金属杆b由静止释放到金属杆a运动到半圆轨道最高点的过程中,系统产生的焦耳热Q。
【答案】(1)![]() (2)
(2)![]()
【解析】(1)金属杆b在倾斜轨道上运动,由动能定理,有: ![]()
![]()
解得: vb1= 2m/s
金属杆b刚滑到水平轨道时速度最大,产生的感应电动势最大,最大值为E= BL vb1
金属杆b中最大电流![]()
受到的最大安培力F安=BIL =Mam
解得:am=0.4 m/s2
(2)金属杆b进入匀强磁场区域后做变速运动,设在Δt时间内,速度变化为Δv金属杆a到达半圆轨道最高点时金属杆b的速度为vb2,则由动量定理有:-BILt=Mv
q=It
v=vb2-vb1
即有: -BLq=Mvb2-Mvb1
解得: vb2=0.4m/s
根据牛顿第三定律得:轨道对金属杆a 向下的压力FN=mg
设金属杆a 运动到半圆轨道最高点的速度为va.由牛顿第二定律,有:
![]()
解得: ![]()
由能量关系有: ![]()
解得:Q = 0.51 J

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案