题目内容
在光滑的水平面上静止着一个质量M = 2kg的绝缘平板小车A(足够长),小车的右端放有质量m = 0.25kg的物体B(视为质点),A不带电,B带正电,电荷量q = 0.25C,竖直MN右边有垂直于纸面向内的匀强磁场(磁场范围足够大),磁感应强度B = 1T,MN距小车右端的距离L = 2m。现对小车施加一水平力F=33N(A、B间有相对运动),当物体B进入磁场时撤去力F,A、B间动摩擦因数μ=0.4,g取10m/s2。求:
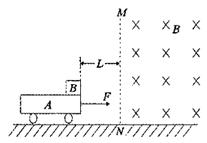
(1)从对小车施加力F开始计时,至小车右端达到MN的时间t;
(2)整个过程中产生的内能。

(1)从对小车施加力F开始计时,至小车右端达到MN的时间t;
(2)整个过程中产生的内能。
(1) 0.5s (2) 18.94J
(1)设小车的加速度为a1,对小车由牛顿第二定律:
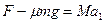 解得:
解得: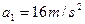
小车进入磁场前有: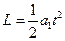
解得: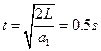
(2)设F作用时间为t0,对物体B:
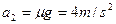
物体进入磁场前有: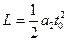
解得: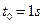
撤去F前,B位移: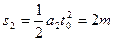
B的速度: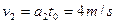
A位移: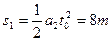
A的速度: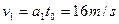
相对位移: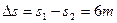
撤去F前系统产生的内能: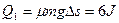
撤去F后,设物体能与小车相对静止,设M、m共同速度大小为v,则由动量守恒定律:
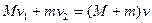
得: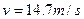
因为 ,所以小车与物体不会相对静止。
,所以小车与物体不会相对静止。
设物体恰好离开小车时的速度为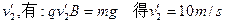
此时小车速度为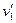 ,则:
,则: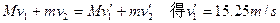
撤去F后系统产生的内能为: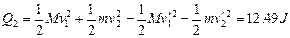
即:整个过程中产生的内能为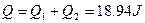
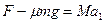 解得:
解得: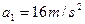
小车进入磁场前有:
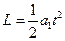
解得:
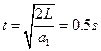
(2)设F作用时间为t0,对物体B:
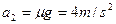
物体进入磁场前有:
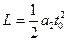
解得:
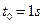
撤去F前,B位移:
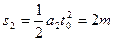
B的速度:
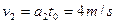
A位移:
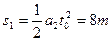
A的速度:
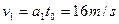
相对位移:
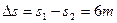
撤去F前系统产生的内能:
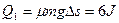
撤去F后,设物体能与小车相对静止,设M、m共同速度大小为v,则由动量守恒定律:
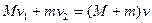
得:
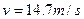
因为
 ,所以小车与物体不会相对静止。
,所以小车与物体不会相对静止。设物体恰好离开小车时的速度为
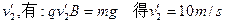
此时小车速度为
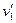 ,则:
,则: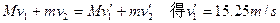
撤去F后系统产生的内能为:
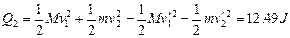
即:整个过程中产生的内能为
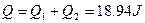

练习册系列答案
相关题目
 、
、 ,其中
,其中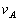 、
、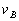 ,在子弹穿透木块过程中因克服摩擦力产生的热分别为
,在子弹穿透木块过程中因克服摩擦力产生的热分别为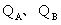 ,设木块对子弹的摩擦力大小一定,则( )
,设木块对子弹的摩擦力大小一定,则( )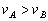 ,
,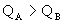
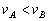 ,
,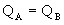
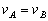 ,
,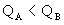




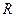 ,
,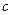 、
、 、
、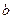 、
、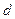 分别是其水平直径和竖直直径的端点.圆环与一个光滑斜轨相接,如图4所示.一个小球从与
分别是其水平直径和竖直直径的端点.圆环与一个光滑斜轨相接,如图4所示.一个小球从与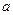 点从斜轨上无初速下滑.试求:
点从斜轨上无初速下滑.试求: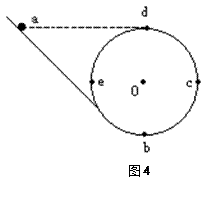
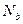 多大?
多大? 多大?如不能,小球于何处离开圆环?
多大?如不能,小球于何处离开圆环?