题目内容
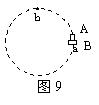
质量不计的细弹簧的劲度系数k="100" N/m，原长L="20" cm，弹簧一端固定一质量m="0.75" kg的小球，以另一端为圆心，使小球在光滑水平面内做线速度v="2" m/s的匀速圆周运动，运动时弹簧与水平面平行，并且形变没有超过弹性限度，求：
(1)小球做圆周运动的角速度;
(2)小球所受弹簧的拉力.
(1)小球做圆周运动的角速度;
(2)小球所受弹簧的拉力.
(1)6.7 rad/s (2)10 N
弹簧的弹力提供了小球做匀速圆周运动的向心力.设弹簧的伸长量为x，则小球做圆周运动的半径为(L+x)，由牛顿第二定律有kx=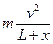
.代入已知数据解得x="0.1" m.
小球做圆周运动的角速度ω=
="6.7" rad/s
小球所受弹簧的拉力F="kx=10" N.
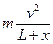.代入已知数据解得x="0.1" m.小球做圆周运动的角速度ω=
="6.7" rad/s小球所受弹簧的拉力F="kx=10" N.
练习册系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
