��Ŀ����
����Ŀ����ͼ��ʾ���綯�����ű����Ĵ��ʹ�ʼ����v=2m/s���ٶ�˳ʱ���˶������ʹ���ˮƽ��ļнǦ�=30�㣬�ְ�һ����Ϊm=10kg�Ĺ�������ط���Ƥ���ĵˣ�����һ��ʱ��������͵���h=2m��ƽ̨�ϣ���֪������Ƥ��֮��Ķ�Ħ��������= ![]() ������֮�⣬����������ģ���gȡ10m/s2����
������֮�⣬����������ģ���gȡ10m/s2����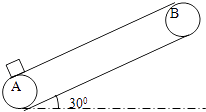
��1�����ʹ����������Ĺ�
��2������������
��3�����ڴ������崫�ʹ������ĵĵ��ܣ�
���𰸡�
��1��
�⣺��������ط��ڴ��ʹ��˺��ܵ�������֧��������б�����ϵ�Ħ�������ã���ţ�ٵڶ����ɵ�֪���ϻ������м��ٶ�Ϊ��
��mgcos�ȩ�mgsin��=ma
�ã�a=g����cos�ȩ�sin�ȣ�=2.5m/s2
�蹤�����ٵ�v0=2m/sʱ�˶���λ��Ϊx�����У�
2ax=v02 �� x=0.8m
�ɵã�x�� ![]() =4m
=4m
���Թ����ڴ��ʹ������ȼ����˶��������˶���
�ȼ����˶������У���Ħ�����Թ�������Ϊ��W1=��mgcos��x=60J
�����˶������ܵ��ľ�Ħ������СΪ��f=mgsin��
ͨ����λ��Ϊ��x��= ![]() ��x=4m��0.8=3.2m
��x=4m��0.8=3.2m
�����˶������У�Ħ�����Թ�������Ϊ��W2=mgsin��x��=160J
����Ħ�����Թ��������ܹ�Ϊ��W=W1+W2=220J
��2��
�⣺����������Q=Ffx���=��mgcos�ȣ�2x��x��=60J
��3��
�⣺�����ĵ�����ת��Ϊ�����Ķ��ܺ����������Լ�Ħ������������
�� ![]() =280J
=280J
����������1��Ҫ�����������˶���������ȷ�����������������������ܵ�������֧��������б�����ϵ�Ħ�������ã�������б�����ϣ���������˶�����ţ�ٵڶ�����������ٶȣ����˶�ѧ��ʽ��������ٶȴﵽ�봫�ʹ���ͬʱͨ����λ�ƣ��ٸ��ݴ�λ���봫�ʹ����ȵĹ�ϵ�������������������˶�����������������̣����ݹ��Ĺ�ʽ���ֱ����Ħ���������������Ĺ�����������ܹ�����2����������������Q=Ffx������㼴�ɣ���3�������ĵ�����ת��Ϊ�����Ķ��ܺ����������Լ�Ħ�����������ܣ�Ȼ����ͼ���
�����㾫����������Ҫ�����˹��ܹ�ϵ�����֪ʶ�㣬��Ҫ���յ�ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1������ȷ�����⣮

 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�