题目内容
18.一只船在静水中的速度为4m/s,它要渡过宽度为300m的一条河;已知水流速度为3m/s,下列说法正确的是( )| A. | 这只船不可能渡过河 | |
| B. | 这只船渡河所用的最短时间为75s | |
| C. | 这只船相对于岸的速度一定是5 m/s | |
| D. | 这只船的实际航线不可能垂直于河岸 |
分析 船在河中参与了沿河方向的运动和本身船速的运动,由运动的合成与分解可分析各选项.
解答 解:A、只要船有向对岸的速度,则船一定可以渡过河,故A错误;
B、当船头正对河岸时时间最短,最短时间为河宽与船速的比值,即$\frac{d}{{v}_{c}}$=$\frac{300}{4}$s=75s,故B正确;
C、根据速度合成法则,只有当船垂直河岸时,船相对于岸的速度才是$\sqrt{{3}^{2}+{4}^{2}}$=5m/s,故C错误;
D、由于船在静水中的速度大于水速,故船可能有垂直于河岸的合速度,故可能垂直于河岸过河,故D错误;
故选:B.
点评 船渡河模型要注意分清合运动与分运动的联系,正确并能灵活利用运动的合成与分解方法,注意能否垂直过河,依据船速与水流速度的大小关系.

练习册系列答案
相关题目
8.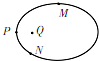 如图所示,带正电的点电荷固定在Q点,一电子仅在库仑力作用下,做以Q点为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.vM、vN和EM、EN分别表示该电子在M、N两点的速度和电势能,则电子从M点逆时针运动到N点( )
如图所示,带正电的点电荷固定在Q点,一电子仅在库仑力作用下,做以Q点为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.vM、vN和EM、EN分别表示该电子在M、N两点的速度和电势能,则电子从M点逆时针运动到N点( )
 如图所示,带正电的点电荷固定在Q点,一电子仅在库仑力作用下,做以Q点为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.vM、vN和EM、EN分别表示该电子在M、N两点的速度和电势能,则电子从M点逆时针运动到N点( )
如图所示,带正电的点电荷固定在Q点,一电子仅在库仑力作用下,做以Q点为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.vM、vN和EM、EN分别表示该电子在M、N两点的速度和电势能,则电子从M点逆时针运动到N点( )| A. | 电子的动能先减小后增大 | B. | 电场力对电子做了负功 | ||
| C. | vM<vN,EM>EN | D. | vM<vN,EM<EN |
9.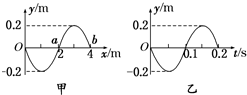 如图甲所示,为一列沿x轴传播的简谐横波在t=0时刻的波形图.图乙表示该波传播的介质中x=2m处的质点a从t=0时刻起的振动图象.则下列说法正确的是( )
如图甲所示,为一列沿x轴传播的简谐横波在t=0时刻的波形图.图乙表示该波传播的介质中x=2m处的质点a从t=0时刻起的振动图象.则下列说法正确的是( )
 如图甲所示,为一列沿x轴传播的简谐横波在t=0时刻的波形图.图乙表示该波传播的介质中x=2m处的质点a从t=0时刻起的振动图象.则下列说法正确的是( )
如图甲所示,为一列沿x轴传播的简谐横波在t=0时刻的波形图.图乙表示该波传播的介质中x=2m处的质点a从t=0时刻起的振动图象.则下列说法正确的是( )| A. | t=0时刻,质点a的振动方向为y轴正方向 | |
| B. | 波沿x轴负方向传播 | |
| C. | t=0.25s时,质点a的位移沿y轴正方向 | |
| D. | t=0.25s时,x=4m处的质点b的加速度沿y轴负方向 |
6.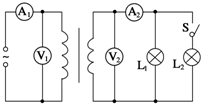 为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
 为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )| A. | A1示数变小,A1与A2示数的比值不变 | |
| B. | A1示数变大,A1与A2示数的比值变大 | |
| C. | V2示数变小,V1与V2示数的比值变大 | |
| D. | V2示数不变,V1与V2示数的比值不变 |
3.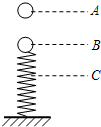 一小球自A点由静止自由下落 到B点时与弹簧接触,到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )
一小球自A点由静止自由下落 到B点时与弹簧接触,到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )
 一小球自A点由静止自由下落 到B点时与弹簧接触,到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )
一小球自A点由静止自由下落 到B点时与弹簧接触,到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )| A. | 小球在B点时动能最大 | |
| B. | 小球的重力势能不断增大 | |
| C. | 小球和弹簧组成的系统机械能守恒 | |
| D. | 到C点时小球重力势能的减少量等于弹簧弹性势能的增加量 |
7.地球赤道上的物体随地球自转的向心加速度为a;假设月球绕地球作匀速圆周运动,轨道半径为r1,向心加速度为a1.已知万有引力常量为G,地球半径为R.下列说法中正确的是( )
| A. | 地球质量M=$\frac{a{R}^{2}}{G}$ | B. | 地球密度$ρ=\frac{{3{a_1}r_1^2}}{{4πG{R^3}}}$ | ||
| C. | 地球的第一宇宙速度为$\sqrt{aR}$ | D. | 向心加速度之比$\frac{{a}_{1}}{a}$=$\frac{{R}^{2}}{{{r}_{1}}^{2}}$ |
8.如图所示的两种交流电分别为正弦交流电和方波交流电,正弦交流电和方波交流电的电流强度的有效值之比为多少( )
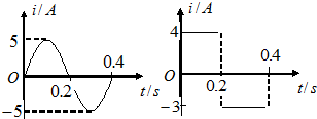
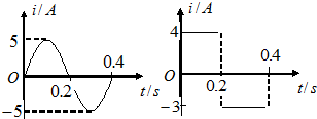
| A. | 1:$\sqrt{2}$ | B. | $\sqrt{2}$:1 | C. | 1:1 | D. | 2:1 |
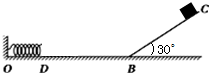 如图所示,水平轨道ODB与一斜面BC平滑相交于B点,斜面BC与水平面的夹角为30°,水平轨道OD段光滑,DB段粗糙,DB段长度L=2m,动摩擦因数?=0.1,BC段光滑且长度S=3.6m,轻质弹簧左端固定于O点,弹簧原长时,右端恰好处于D点.现把质量m=2kg的可视为质点的小滑块由C点静止释放,沿CB下滑,进入水平轨道继续滑行后压缩弹簧,设滑块在经过B点瞬间速率大小不变(取g=10m/s2,空气阻力不计).
如图所示,水平轨道ODB与一斜面BC平滑相交于B点,斜面BC与水平面的夹角为30°,水平轨道OD段光滑,DB段粗糙,DB段长度L=2m,动摩擦因数?=0.1,BC段光滑且长度S=3.6m,轻质弹簧左端固定于O点,弹簧原长时,右端恰好处于D点.现把质量m=2kg的可视为质点的小滑块由C点静止释放,沿CB下滑,进入水平轨道继续滑行后压缩弹簧,设滑块在经过B点瞬间速率大小不变(取g=10m/s2,空气阻力不计).