题目内容
 (2012?广东二模)如图,一物块以150J的初动能从斜面底端A沿斜面向上滑动,到B时动能减少90J,机械能减少30J.
(2012?广东二模)如图,一物块以150J的初动能从斜面底端A沿斜面向上滑动,到B时动能减少90J,机械能减少30J.求:(1)第一次到达最高点时的重力势能为多少?(取斜面底端为零势点)
(2)若回到A时和挡板相碰无能量损失,物块运动过程中通过的总路程为多少?(设物块质量为1kg,斜面倾角为30°,g=10m/s2)
分析:(1)克服摩擦力做功与克服重力做功的比值一定,根据动能定理 WfB+WGB=△Ek,求出克服重力做功以及克服摩擦力做功,从而得出它们的比值,再对从A上升到最高点运用动能定理,根据克服摩擦力做功和克服重力做功的比值求出克服重力做功的大小,从而得出最高点的重力势能.
(2)根据克服重力做功和克服摩擦力做功的比值求出动摩擦因数,物体最终会停在挡板处,对全过程运用动能定理,求出物体运动的总路程.
(2)根据克服重力做功和克服摩擦力做功的比值求出动摩擦因数,物体最终会停在挡板处,对全过程运用动能定理,求出物体运动的总路程.
解答: 解:(1)设斜面倾角为θ,物体上滑s的位移,
解:(1)设斜面倾角为θ,物体上滑s的位移,
摩擦力做功为Wf=-μmgscosθ=-μmgL(L为s在水平方向上的投影)
重力势能增加Ep=mgh
则
=μ
=μcotθ,当斜面倾角不变时,摩擦力做的功与重力势能增量的比值一定.
设从A点到最高点,摩擦力做功为Wf,在最高点重力势能为Ep
物体从A到B由动能定理得 WfB+WGB=△Ek
WfB=△E机
由题意得△Ek=-90J,△E机=-30J,联立得EpB=60J
则有
=
=
从A点到最高点由动能定理,有|Wf|+Ep=150,联立解得Ep=100J
(2)由(1)知μcotθ=
=
,则μ=
因为mgsin30°>μmgcos30°,因此物体最终会停在挡板处,设总路程为S总,则由动能定理,得
-μmgS总cos30°=0-Ek0,
解得S总=60m
答:(1)第一次到达最高点时的重力势能为100J.
(2)若回到A时和挡板相碰无能量损失,物块运动过程中通过的总路程为60m.
 解:(1)设斜面倾角为θ,物体上滑s的位移,
解:(1)设斜面倾角为θ,物体上滑s的位移,摩擦力做功为Wf=-μmgscosθ=-μmgL(L为s在水平方向上的投影)
重力势能增加Ep=mgh
则
| |Wf| |
| Ep |
| L |
| h |
设从A点到最高点,摩擦力做功为Wf,在最高点重力势能为Ep
物体从A到B由动能定理得 WfB+WGB=△Ek
WfB=△E机
由题意得△Ek=-90J,△E机=-30J,联立得EpB=60J
则有
| |Wf| |
| Ep |
| |WfB| |
| EpB |
| 1 |
| 2 |
从A点到最高点由动能定理,有|Wf|+Ep=150,联立解得Ep=100J
(2)由(1)知μcotθ=
| |WfB| |
| EpB |
| 1 |
| 2 |
| ||
| 6 |
因为mgsin30°>μmgcos30°,因此物体最终会停在挡板处,设总路程为S总,则由动能定理,得
-μmgS总cos30°=0-Ek0,
解得S总=60m
答:(1)第一次到达最高点时的重力势能为100J.
(2)若回到A时和挡板相碰无能量损失,物块运动过程中通过的总路程为60m.
点评:解决本题的关键得出克服阻力做功和克服重力做功的比值一定,运用动能定理进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012?广东二模)如图所示,放在水平面上的物体受到一个水平向右的拉力F作用处于静止状态,下列说法中正确的是( )
(2012?广东二模)如图所示,放在水平面上的物体受到一个水平向右的拉力F作用处于静止状态,下列说法中正确的是( ) (2012?广东二模)如图所示,光滑水平桌面上,有甲、乙两个用轻质细线相连的物体在水平拉力F1和F2的作用下运动,已知F1<F2,则以下说法中正确的有( )
(2012?广东二模)如图所示,光滑水平桌面上,有甲、乙两个用轻质细线相连的物体在水平拉力F1和F2的作用下运动,已知F1<F2,则以下说法中正确的有( )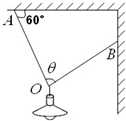 (2012?广东二模)如图所示,用一根细线OB把电灯拉至图中位置,电线OA与天花板夹角为60°.若要使细线OB所受拉力最小,则细绳OB与OA的夹角θ应为( )
(2012?广东二模)如图所示,用一根细线OB把电灯拉至图中位置,电线OA与天花板夹角为60°.若要使细线OB所受拉力最小,则细绳OB与OA的夹角θ应为( )