题目内容
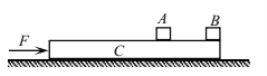
【题目】如图所示,在光滑水平面上静止放置质量M=2kg、长L=2.17m、高h=0.2m的长木板C。距该板左端距离x=1.81m处静止放置质量mA=1kg的小物块A,A与C间的动摩擦因数μ=0.2。在板右端静止放置质量mB=1kg的小物块B,B与C间的摩擦忽略不计。A、B均可视为质点,设最大静摩擦力等于滑动摩擦力,g取10m/s2。现在长木板C上加一水平向右的力F,求:
(1)当F=3N时,小物块A的加速度;
(2)小物块A与小物块B碰撞之前运动的最短时间;
(3)若小物块A与小物块B碰撞之前运动的时间最短,则水平向右的力F的大小(本小题计算结果保留整数部分);
(4)若小物块A与小物块B碰撞无能量损失,当水平向右的力F=10N,小物块A落到地面时与长木板C左端的距离。
【答案】(1)1m/s2;(2)t=0.6s;(3)6N≤F≤26N;(4)x2=0.78m
【解析】
(1)若长木板C和小物块一起向右加速运动,设它们之间是静摩擦力为f,由牛顿第二定律得:
F=(M+mA)a
解得
a=1m/s2
则f=mAa=1N<μmAg=2N,这表明假设正确,即A的加速度为1m/s2
(1)要使小物块A在与小物块B碰撞之前运动时间最短,小物块A的加速度必须最大,则A所受的摩擦力为最大静摩擦力或滑动摩擦力,有
μmAg=mAa1
![]()
解得
t=0.6s
(3)要使小物块A加速度最大,且又不从长木板C的左端滑落,长木板C的加速度有两个临界条件:
①由牛顿第二定律得:
F1=(M+mA)a1
则
F1=6N
②由牛顿第二定律得:
F2-f=Ma2
![]()
则
F2=26N
故6N≤F≤26N
(4)若小物块A与小物块B碰撞点距从长木板C的左端距离为x1
F3-f=Ma3
![]()
解得
x1=1.45m
设小物块A发生碰撞到从长木板C左端滑落的时间为t1,因有物块A、B发生弹性碰撞,速度交换,故有
![]()
解得
t1=0.5s
设小物块A碰撞到从长木板C左端滑落时各自的速度分别为vm、vM,小物块A落到地面时与长木板C左端的距离为x2
![]()
F3=Ma4
vm=a1t1
vM=a3t+a3t1
则有
vMt2+![]() -vmt2=x2
-vmt2=x2
x2=0.78m

 名校课堂系列答案
名校课堂系列答案