题目内容
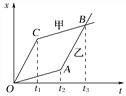
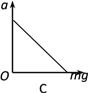
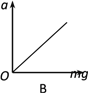
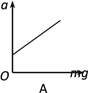
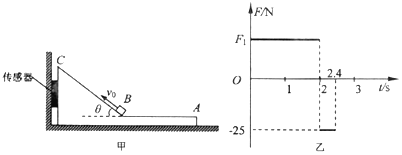
【题目】如图甲所示,带有斜面的木块放在光滑水平地面上,木块水平表面AB粗糙,斜面BC表面光滑且与水平面夹角为θ=37°,木块左侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值,当力传感器被拉时,其示数为负值,一个可视为质点的质量m=5kg的滑块从B点以初速度v0沿斜面向上运动,运动整个过程中,传感器记录到的力与时间的关系如图乙所示,已知斜面足够长,设滑块经过B点时无机械能损失,g取10m/s2。求:
(1)图乙中F1的数值大小;
(2)滑块的初速度v0;
(3)水平表面AB的长度 。
【答案】(1)24N;(2)6m/s;(3)2m
【解析】
(1)根据牛顿第二定律计算滑块沿斜面向上运动时的加速度,根据运动的合成与分解计算水平方向的分加速度,根据牛顿第二定律图乙中F1的数值大小;(2)根据速度时间关系初速度大小;(3)根据牛顿第二定律可得滑块在水平部分的加速度大小,根据位移时间关系求解水平表面AB的长度.
(1)质量为m=5kg的滑块沿斜面向上运动时的加速度大小为:![]()
水平方向的分加速度为![]()
水平方向斜面对滑块的作用力为![]()
根据牛顿第三定律可得:![]()
(2)经过时间t=1s到达最高点,根据速度时间关系可得:![]()
(3)根据图象可知,滑块在水平部分运动的摩擦力大小为![]()
根据牛顿第二定律可得加速度大小为:![]()
滑块在水平部分运动的时间为:![]()
根据位移时间关系可得:![]()

练习册系列答案
相关题目