��Ŀ����
16��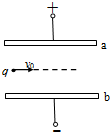 ������е������ֵ�ɵĽ����忿��ʱ���������Ե��������������糡ǿ�ȵĴ�С��������ͬ�ĵ糡��������ǿ�糡����ͼ��ʾ��ˮƽ���õ�ƽ�н�����a��b����һ��ǿ�糡��һ����Ϊq=4��10-6C������Ϊm=2.5��10-3kg�Ĵ���Һ�Σ���ˮƽ���ٶ�v0����������˷���糡��Һ��ǡ��������ˮƽֱ�߷���a��b�����ǿ�糡����Һ�δ����ֵ�ɸ�������������a��b���������ǿ�糡�ij�ǿΪ6250 N/C��
������е������ֵ�ɵĽ����忿��ʱ���������Ե��������������糡ǿ�ȵĴ�С��������ͬ�ĵ糡��������ǿ�糡����ͼ��ʾ��ˮƽ���õ�ƽ�н�����a��b����һ��ǿ�糡��һ����Ϊq=4��10-6C������Ϊm=2.5��10-3kg�Ĵ���Һ�Σ���ˮƽ���ٶ�v0����������˷���糡��Һ��ǡ��������ˮƽֱ�߷���a��b�����ǿ�糡����Һ�δ����ֵ�ɸ�������������a��b���������ǿ�糡�ij�ǿΪ6250 N/C��
���� ��1������Һ��ǡ����ˮƽֱ���˶������е糡��������ƽ�⣬�����ɵ糡ǿ�ȵķ���ȷ��Һ�δ����ԣ�
��2���ɵ糡����������������$E=\frac{F}{q}$��������⣻
��� �⣺��1������Һ�Σ�����ƽ�⣬���е糡����ֱ���ϣ�
����糡ǿ�ȷ������£�����Һ�δ����磻
��2����������ƽ�⣬����Eq=mg
���� E=$\frac{mg}{q}=\frac{2.5��1{0}^{-3}��10}{4��1{0}^{-6}}$N/C=6250 N/C
�ʴ�Ϊ������6250
���� ���������ڵ糡������ƽ�⣬��ƽ������ȷ���糡������ϵ糡ǿ�ȵķ�����ȷ����ɵĵ���

��ϰ��ϵ�д�
 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
�����Ŀ
8��һ��שͷ��24cm����12cm����6cm����Ϊ20N����שƽ����ˮƽ���棬��һ��8N��ˮƽ���պ��ܹ����������ֽ�שͷ�����ˮƽ����ʱ��Ҫʹ��ˮƽ�ƶ�����Ҫ��ˮƽ����СΪ��������
| A�� | 16N | B�� | 12N | C�� | 8N | D�� | 4N |
7�� ��ͼ��ʾ������ƽ�е��㹻���Ĺ⻬����ֱ����ļ��ΪL����ˮƽ��ɦȽǣ�����װ�ô��ڴ�ֱ����ƽ�����ϴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų��У�����������Ϊm�������ΪR����ͬԲ���嵼���ab��cd��ֱ�ڵ�����ã����������챣�����ýӴ��������һ��б�����ϵĺ���F������ab��ʹ���Ӿ�ֹ��ʼ�ع�����ϼ����˶���ͬʱ�ſ�cd�ˣ����۲췢�֣���ab�˼��ٵ�����V1��ͬʱcd�˵�������V2��б�������˶������Ҵ˺����˶���ʼ�������˶������������ٶȴ�СΪg�����������й����������������й��ж���ȷ���У�������
��ͼ��ʾ������ƽ�е��㹻���Ĺ⻬����ֱ����ļ��ΪL����ˮƽ��ɦȽǣ�����װ�ô��ڴ�ֱ����ƽ�����ϴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų��У�����������Ϊm�������ΪR����ͬԲ���嵼���ab��cd��ֱ�ڵ�����ã����������챣�����ýӴ��������һ��б�����ϵĺ���F������ab��ʹ���Ӿ�ֹ��ʼ�ع�����ϼ����˶���ͬʱ�ſ�cd�ˣ����۲췢�֣���ab�˼��ٵ�����V1��ͬʱcd�˵�������V2��б�������˶������Ҵ˺����˶���ʼ�������˶������������ٶȴ�СΪg�����������й����������������й��ж���ȷ���У�������
 ��ͼ��ʾ������ƽ�е��㹻���Ĺ⻬����ֱ����ļ��ΪL����ˮƽ��ɦȽǣ�����װ�ô��ڴ�ֱ����ƽ�����ϴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų��У�����������Ϊm�������ΪR����ͬԲ���嵼���ab��cd��ֱ�ڵ�����ã����������챣�����ýӴ��������һ��б�����ϵĺ���F������ab��ʹ���Ӿ�ֹ��ʼ�ع�����ϼ����˶���ͬʱ�ſ�cd�ˣ����۲췢�֣���ab�˼��ٵ�����V1��ͬʱcd�˵�������V2��б�������˶������Ҵ˺����˶���ʼ�������˶������������ٶȴ�СΪg�����������й����������������й��ж���ȷ���У�������
��ͼ��ʾ������ƽ�е��㹻���Ĺ⻬����ֱ����ļ��ΪL����ˮƽ��ɦȽǣ�����װ�ô��ڴ�ֱ����ƽ�����ϴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų��У�����������Ϊm�������ΪR����ͬԲ���嵼���ab��cd��ֱ�ڵ�����ã����������챣�����ýӴ��������һ��б�����ϵĺ���F������ab��ʹ���Ӿ�ֹ��ʼ�ع�����ϼ����˶���ͬʱ�ſ�cd�ˣ����۲췢�֣���ab�˼��ٵ�����V1��ͬʱcd�˵�������V2��б�������˶������Ҵ˺����˶���ʼ�������˶������������ٶȴ�СΪg�����������й����������������й��ж���ȷ���У�������| A�� | F=mgsin��+$\frac{{B}^{2}{L}^{2}{V}_{1}}{2R}$ | |
| B�� | $\frac{{B}^{2}{L}^{2}��{V}_{1}+{V}_{2}��}{R}$=2mgsin�� | |
| C�� | F�����Ĺ�����ab�˻�е�ܵ�����������������6�����Ľ�����֮�� | |
| D�� | �����˴ﵽ����֮����еĵ���ǿ��I=$\frac{mgsin��}{BL}$ |
4������˵������ȷ���ǣ�������
| A�� | �����ں��������²������������˶� | |
| B�� | �����ڱ��������¿����������˶� | |
| C�� | �������˶������壬���ٶȷ�������ٶȵķ�����ͬһֱ���� | |
| D�� | ����ͨ��Ť��ʵ�飬�ⶨ���������������� |
6��2013��12��2��1ʱ30�֣��ҹ����������Ƿ��������á����������ҡ����ػ�ǰ���ɹ������϶����š�̽��ɴ����գ�չ������֮�ã����϶����š��״�ʵ������Ѳ�ӿ������������½��Ϊ�ҹ�̽�¹��̿����µ����̣������ŵ��²յ�̽��ɴ�������������ΪԲ�ģ��뾶Ϊr1��Բ���������ʱ������ΪT1�������²�����ɴ�����쵽����������İ뾶Ϊr2��Բ��������У�������ΪG��������˵����ȷ���ǣ�������
| A�� | ���²��ڰ뾶Ϊr2��Բ����ϱ��ڰ뾶Ϊr1��Բ��������ʱ�Ľ��ٶȴ� | |
| B�� | ���²��ڰ뾶Ϊr2��Բ����ϱ��ڰ뾶Ϊr1��Բ��������ʱ�����ٶȴ� | |
| C�� | ���������Ϊ$\frac{{4{��^2}r_1^3}}{GT_1^2}$ | |
| D�� | ���²��ڰ뾶Ϊr2��Բ���������ʱ������Ϊ${\;}^3\sqrt{{\frac{r_2^2T_1^3}{r_1^2}}}$ |
 ��ͼ��ʾ��ij�������������Ĺ��ijһ�Σ��Ż����Ƶ�������������Ϊ�ʵ㣩������m=1.0kg�������ΪP=7W���Ż�������������ˮƽƽ̨��A��ʱ�ٶȺ�С������Ϊ0������ʱ�����������ķ�������ֱ��ʹ�������Ĺ��ʴﵽ����ʣ�һ��ʱ���رշ�����������������ƽ̨��ԵB��ɳ���ǡ������ֱ�⻬Բ�����CDE��C������߷������Բ�ι�����Ҵ�ʱ���ٶȴ�СΪ5m/s����COD=53�㣬���ӹ����ԵE����ֱ���Ϸɳ����뿪E�Ժ����������߶�Ϊh=0.85m����֪AB��ľ���L=6m����������AB���˶�ʱ��������Ϊ1N���������ٶ�gȡ10m/s2�����ƿ���������sin53��=0.8��cos53��=0.6����
��ͼ��ʾ��ij�������������Ĺ��ijһ�Σ��Ż����Ƶ�������������Ϊ�ʵ㣩������m=1.0kg�������ΪP=7W���Ż�������������ˮƽƽ̨��A��ʱ�ٶȺ�С������Ϊ0������ʱ�����������ķ�������ֱ��ʹ�������Ĺ��ʴﵽ����ʣ�һ��ʱ���رշ�����������������ƽ̨��ԵB��ɳ���ǡ������ֱ�⻬Բ�����CDE��C������߷������Բ�ι�����Ҵ�ʱ���ٶȴ�СΪ5m/s����COD=53�㣬���ӹ����ԵE����ֱ���Ϸɳ����뿪E�Ժ����������߶�Ϊh=0.85m����֪AB��ľ���L=6m����������AB���˶�ʱ��������Ϊ1N���������ٶ�gȡ10m/s2�����ƿ���������sin53��=0.8��cos53��=0.6����