题目内容
6.2013年12月2日1时30分,我国在西昌卫星发射中心用“长征三号乙”运载火前,成功将“嫦娥三号”探测飞船升空,展开奔月之旅.“嫦娥三号”首次实现月面巡视勘察和月球软着陆,为我国探月工程开启新的征程.设载着登月舱的探测飞船在以月球中心为圆心,半径为r1的圆轨道上运行时,周期为T1.随后登月舱脱离飞船,变轨到离月球更近的半径为r2的圆轨道上运行.引力常为G,则下列说法正确的是( )| A. | 登月舱在半径为r2的圆轨道上比在半径为r1的圆轨上运行时的角速度大 | |
| B. | 登月舱在半径为r2的圆轨道上比在半径为r1的圆道上运行时的线速度大 | |
| C. | 月球的质量为$\frac{{4{π^2}r_1^3}}{GT_1^2}$ | |
| D. | 登月舱在半径为r2的圆轨道上运行时的周期为${\;}^3\sqrt{{\frac{r_2^2T_1^3}{r_1^2}}}$ |
分析 根据万有引力提供向心力,得到卫星的速度公式,分析登月舱在两种轨道上速度的大小.由v=ωr,分析角速度的关系;
根据万有引力等于向心力,由万有引力定律和向心力公式列式,可求出月球的质量.根据开普勒第三定律,化简可得登陆舱在半径为r2轨道上的周期.
解答 解:A、万有引力提供登月舱做圆周运动的向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,G$\frac{Mm}{{r}^{2}}$=mω2r,解得:v=$\sqrt{\frac{GM}{r}}$,ω=$\sqrt{\frac{GM}{{r}^{3}}}$,可知卫星的轨道半径越小,角速度和线速度越大,所以登月舱在半径为r2的圆轨道上比在半径r1的圆轨道上运动时的角速度、线速度都大,故AB正确.
C、登月舱在半径为r1的圆轨道上运动时,由G$\frac{Mm}{{r}_{1}^{2}}$=m($\frac{2π}{{T}_{1}}$)2r1,则得月球的质量为:M=$\frac{4{π}^{2}{r}_{1}^{3}}{G{T}_{1}^{2}}$,故C正确.
D、根据开普勒第三定律有:$\frac{{T}_{1}^{2}}{{T}_{2}^{2}}$=$\frac{{r}_{1}^{3}}{{r}_{2}^{3}}$,可得:T2=$\sqrt{\frac{{r}_{2}^{3}}{{r}_{1}^{3}}}$T1,故D错误.
故选:ABC.
点评 本题是典型的天体运动的问题,根据万有引力提供向心力是解决这类问题常用思路,要能根据题目的要求熟练选择不同的向心力的表达式.

练习册系列答案
相关题目
17.2011年9月29日21时16分我国第一个空间实验室“天宫一号”发射升空,并成功进入约350公里的圆轨道,绕行485圈后,降轨至高度约为343公里的圆轨道.11月24日发射的在近地点200公里、远地点330公里的预定轨道飞行的“神舟八号”飞船与“天宫一号”成功对接.关于“天宫一号”与“神舟八号”的说法正确的是( )
| A. | “神舟八号”与“天宫一号”在对接前相比较,“神舟八号”的运行周期小于“天宫一号”的运行周期 | |
| B. | “天宫一号”降轨前的速度小于同步卫星的速度 | |
| C. | “天宫一号”降轨后与降轨前相比动能增大、势能减小、机械能增大 | |
| D. | “神舟八号”飞船必须在半径大于343公里的轨道加速才能与“天宫一号”对接 |
1.关于电阻率的说法正确的是( )
| A. | 电阻率与导体的长度和横截面积有关 | |
| B. | 电阻率表征了材料导电能力的强弱,由导体的材料决定,且与温度有关 | |
| C. | 电阻率大的导体电阻一定大 | |
| D. | 有些合金的电阻率几乎不受温度变化的影响,用它们可做成定值电阻 |
11.在如图电路中,电源的电动势是E,内电阻是r,当滑动变阻器R3的滑动头向左移动时( )
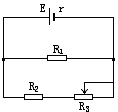

| A. | 电阻R1两端的电压将增大 | B. | 电阻R2两端的电压将增大 | ||
| C. | 总电流将减小 | D. | 流过R3的电流将减小 |
16.一个做直线运动的物体受到的合外力的方向与物体运动的方向一致,当合外力增大时,则物体运动的加速度和速度的变化是( )
| A. | 加速度增大 | B. | 加速度减小 | C. | 速度增大 | D. | 速度减小 |
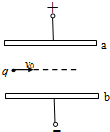 两块带有等量异种电荷的金属板靠近时,互相正对的中央区域会产生电场强度的大小、方向处处相同的电场,叫做匀强电场.如图所示,水平放置的平行金属板a、b间有一匀强电场.一电量为q=4×10-6C、质量为m=2.5×10-3kg的带电液滴,以水平初速度v0,从两板左端飞入电场,液滴恰能匀速沿水平直线方向穿出a、b间的匀强电场区域,液滴带何种电荷负(正、负),a、b金属板间匀强电场的场强为6250 N/C.
两块带有等量异种电荷的金属板靠近时,互相正对的中央区域会产生电场强度的大小、方向处处相同的电场,叫做匀强电场.如图所示,水平放置的平行金属板a、b间有一匀强电场.一电量为q=4×10-6C、质量为m=2.5×10-3kg的带电液滴,以水平初速度v0,从两板左端飞入电场,液滴恰能匀速沿水平直线方向穿出a、b间的匀强电场区域,液滴带何种电荷负(正、负),a、b金属板间匀强电场的场强为6250 N/C.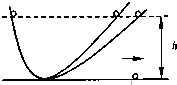 理想实验有时更能深刻地反映自然规律,伽利略设想了一个理想实验,其中有一个是经验事实,其余是推论.如图所示:
理想实验有时更能深刻地反映自然规律,伽利略设想了一个理想实验,其中有一个是经验事实,其余是推论.如图所示: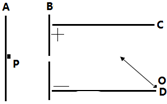 如图所示,C、D两带电平行金属板间的电压为U,A、B也为一对竖直放置的带电平行金属板,B板上有一小孔,小孔在C、D两板间的中心线上.一质量为m、带电量为+q的粒子(不计重力)从D板边缘的O点以速度vo斜向射入C、D板间,穿过B板的小孔运动到紧靠A板的P点时速度恰好为零,则A、B两板间的电压为多少?
如图所示,C、D两带电平行金属板间的电压为U,A、B也为一对竖直放置的带电平行金属板,B板上有一小孔,小孔在C、D两板间的中心线上.一质量为m、带电量为+q的粒子(不计重力)从D板边缘的O点以速度vo斜向射入C、D板间,穿过B板的小孔运动到紧靠A板的P点时速度恰好为零,则A、B两板间的电压为多少?